Алгоритм А* — один из самых эффективных алгоритмов поиска кратчайшего пути между двумя точками графа. Он был опубликован Питером Хартом, Нильсом Нильссоном и Бертрамом Рафаэлем в 1968 году. В каком-то смысле его можно назвать расширением алгоритма Дейкстры. Однако, несмотря на это он является одним из самых часто используемых алгоритмов поиска пути.
Говоря простым языком, алгоритм А* находит оптимальный вариант благодаря вычислению суммарной стоимости всех путей между начальной и конечной точкой. Кстати, этот способ быстрее алгоритма Дейкстры благодаря эвристической функции.
- f(n) = g(n) + h(n)
- f(n): общая стоимость пути
- g(n): стоимость пути между текущей и начальной вершиной
- h(n): эвристическая функция
Разберем пример. У нас есть граф:
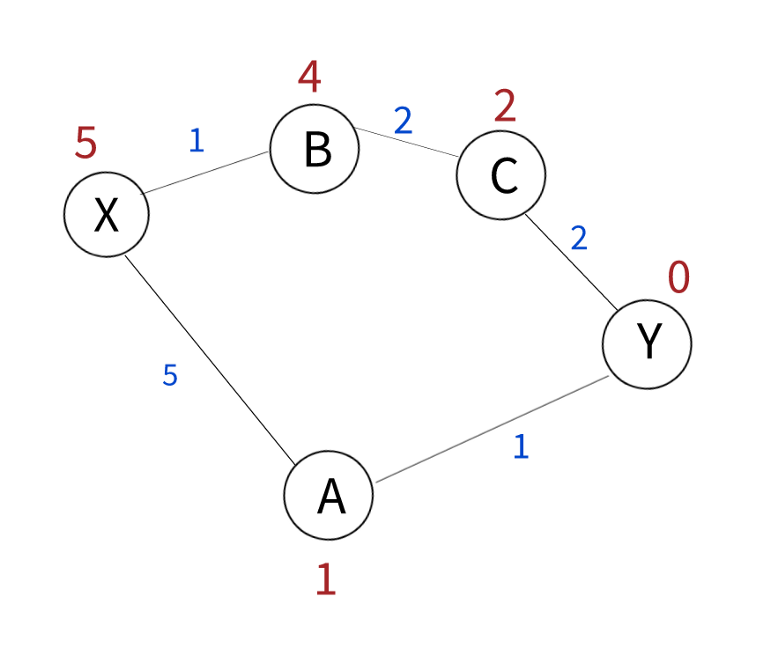
Допустим, мы хотим попасть из точки X в точку Y. Так как вершина Х не меняет своего положения, мы можем отбросить g(n) — ее значение равно 0. Эвристическое значение этой вершины выделено красным шрифтом — 5.
В подобных задачах эвристическое значение — стоимость достижения рассматриваемой вершины из начальной.
Из вершины Х есть два пути.
Если мы перейдем в вершину А, g(n) будет равна 5 (стоимость пути), так как мы перемещаемся в новую вершину. Значение h(n) теперь равно 1. Значение f(n) в точке А будет равно 5+1 = 6. Теперь найдем значение f(n) каждой точки:
- X— A => g(A) + f(A) = 5 + 1 = 6,
- A — Y=> g(Y) + f(Y) = 6+ 0= 6,
- X— B => g(B) + f(B) = 1+ 4= 5,
- B — C => g(C) + f(C) = 3+ 2= 5,
- C — Y=> g(Y) + f(Y) = 5 + 0= 5,
Как видно из наших вычислений, кратчайший путь — X-B-C-Y. Его стоимость равна 5, в то время как X-A-Y — 6. С этим примером разобрались, рассмотрим следующий.
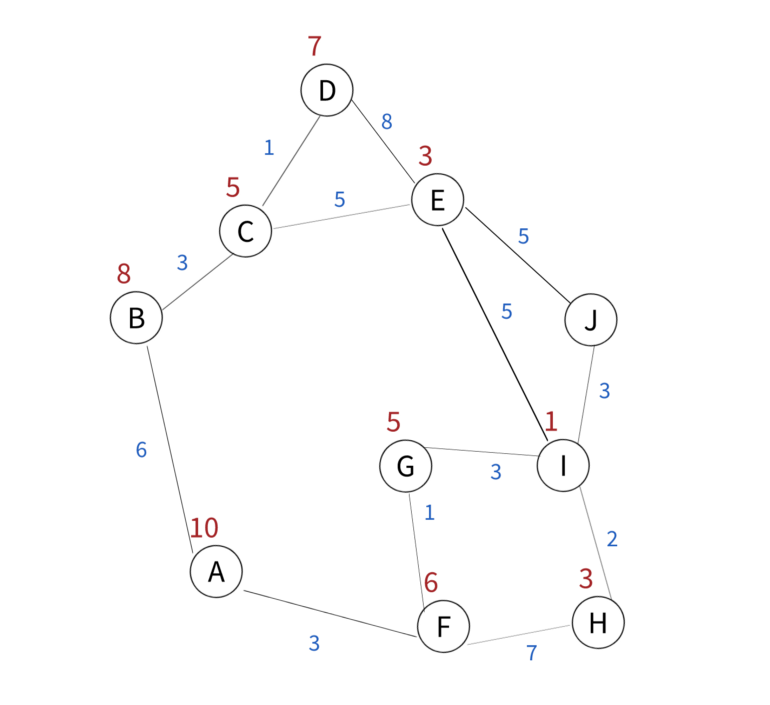
Допустим, мы хотим найти кратчайший путь от вершины А до вершины J.
Из А есть только два пути — B и F. Вычислим стоимость: f(B) = 8 + 6 = 14 и f(F) = 3+6 =9. Следовательно, нам нужно перейти в вершину F — алгоритм продолжит работу отсюда.
Из точки F есть два пути — G и H. Снова вычислим стоимость: f(G) = 4 +5 = 9 and f(H) = 10 + 3 = 13. Значит, мы переходим в точку G.
Следуя пути I—J, получаем следующее: f(I) = 7 + 1 = 8 и f(J) = 10. Так как все значения, следующие за вершиной F, меньше f(B), возвращаться к вершине B не имеет смысла.
Но допустим другой вариант. Предположим, что f(I) больше f(B) при прохождении через F и G (f(I) > 14). В этом случае алгоритм A* прекратит дальнейшую работу и переместится в вершину В. Но, так как f(C) > f(I), работа алгоритма продолжается именно в вершине I.
Реализация алгоритма на Python
Весь проект по визуализации алгоритма, со всеми файлами и полным кодом доступен в репозитории.
Для начала нам нужно создать сетку. Некоторые узлы отметим как препятствия. После этого выбираем начальную и конечную вершину — и запускаем алгоритм!
Логика алгоритма основана на двух списках — open_set и closed_set. Обратите внимание, что вершины в этих двух списках не должны повторяться! (При некоторых подходах препятствия сразу же помещаются в closed_set, а при других рассматриваются как возможные варианты). В результате работы алгоритма эти списки опустошаются и заполняются и в итоге достигается результат.
def main(self):
grid = AStar.create_grid(self.cols, self.rows)
grid = AStar.fill_grids(grid, self.cols, self.rows, obstacle_ratio = self.obstacle_ratio, obstacle_list = self.obstacle_list)
grid = AStar.get_neighbors(grid, self.cols, self.rows)
open_set = []
closed_set = []
current_node = None
final_path = []
open_set.append(grid[self.start[0]][self.start[1]])
self.end = grid[self.end[0]][self.end[1]]
while len(open_set) > 0:
open_set, closed_set, current_node, final_path = AStar.start_path(open_set, closed_set, current_node, self.end)
if len(final_path) > 0:
break
return final_path
Псевдокод вы можете найти в Википедии.
В репозитории проекта есть GIF-ка, наглядно демонстрирующая работу алгоритма А*. Для визуализации использована библиотека Pyp5js.
Работая с этим алгоритмом, можно указать список с препятствиями, координаты начальной и конечной вершины, размер сетки. Следовательно, данную реализацию можно использовать для решения различных задач.
python AStar.py -c 25 -r 25 -s 1 -q 3 -e 23 -t 21 -l True
В результате получаем:
The way found!!! 23 20 23 19 23 18 23 17 23 16 23 15 23 14 23 13 23 12 23 11 23 10 23 9 23 8 23 7 23 6 23 5 23 4 23 3 22 3 21 3 20 3 19 3 18 3 17 3 16 3 15 3 14 3 13 3 12 3 11 3 10 3 9 3 8 3 7 3 6 3 5 3 4 3 3 3 2 3 1 3
Pyp5js
Pyp5js — это фреймворк для визуализации программ, написанных на Python, прямо в браузере! С его помощью запускается JavaScript-библиотека p5.js. После установки фреймворк запускается следующей командой:
$ SKETCHBOOK_DIR='~/my-custom-sketchbook' pyp5js serve
После этого все, что нужно, настраивается в интерфейсе по адресу http://localhost:5000/. В папке SKETCHBOOK_DIR все операции осуществляются в соответствии с Python-кодом в файле, имя которого совпадает с именем проекта.
Итоги
Алгоритм А* — один из самых часто используемых алгоритмов поиска кратчайшего пути. В этой статье мы разобрали принципы его работы и обсудили его реализацию на Python. Для визуализации мы использовали библиотеку pyp5js.

