Алгоритмы сортировки на Python

В этой статье мы вкратце расскажем, какие есть основные алгоритмы сортировки и каковы их главные характеристики. Также по каждому алгоритму покажем реализацию на Python.

Искусство наведения порядка

Сортировка означает размещение элементов в определенном порядке. Этот конкретный порядок определяется свойством сравнения элементов. В случае целых чисел мы говорим, что сначала идет меньшее число, а потом — большее.

Расположение элементов в определенном порядке улучшает поиск элемента. Следовательно, сортировка широко используется в информатике.

В данной статье мы рассмотрим обычные алгоритмы сортировки и их реализации на Python. Для сравнения их производительности мы будем рассматривать задачу с сайта Leetcode о сортировке массива. Размеры данных этой задачи ограничены следующим образом:

1 <= nums.length <= 50000
-50000 <= nums[i] <= 50000

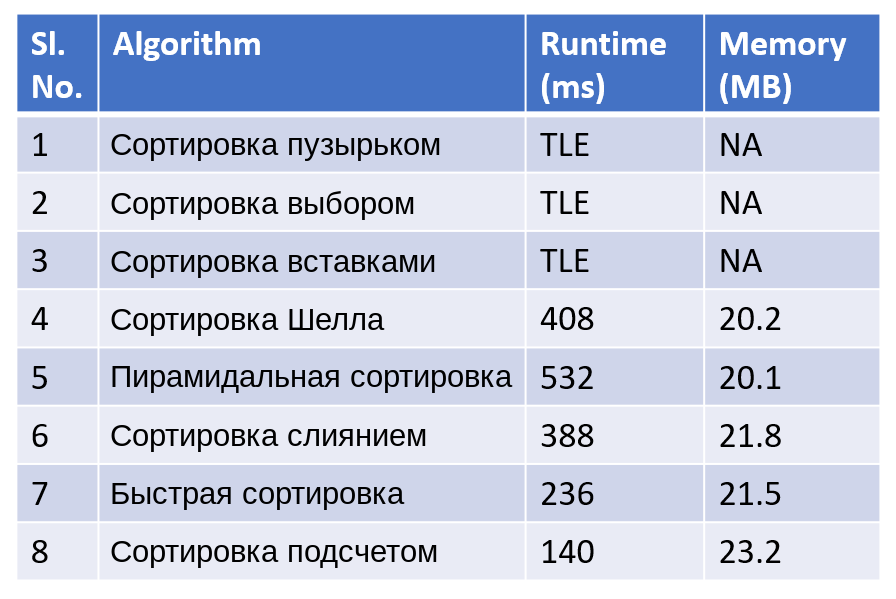
Мы решили эту задачу при помощи всех известных алгоритмов сортировки. Вот какие у нас получились результаты:

Сортировка методом пузырька

Это самый простой алгоритм сортировки. В процессе его выполнения мы перебираем наш список и на каждой итерации сравниваем элементы попарно. При необходимости элементы меняются местами, чтобы больший элемент отправлялся в конец списка.

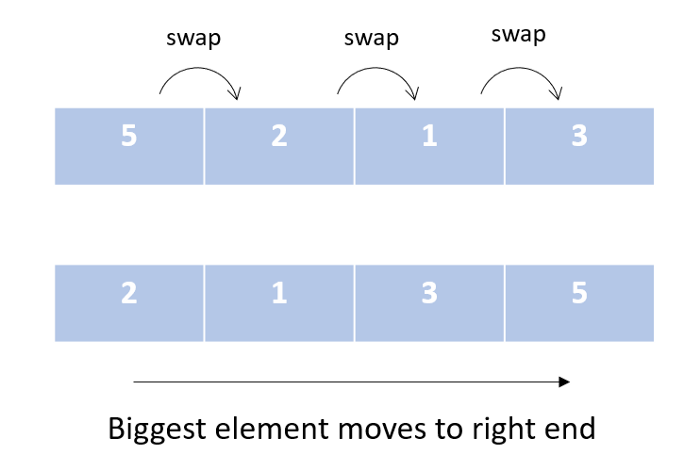
Алгоритм сортировки пузырьком:

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n²);

def bubbleSort(array):
    swapped = False
    for i in range(len(array)-1,0,-1):
        for j in range(i):
            if array[j]>array[j+1]:
                array[j], array[j+1] = array[j+1], array[j]
                swapped= True
        if swapped:
            swapped=False
        else:
            break
    return array

Сортировка выбором

В этом алгоритме мы создаем два сегмента нашего списка: один отсортированный, а другой несортированный.

В процессе выполнения алгоритма мы каждый раз удаляем самый маленький элемент из несортированного сегмента списка и добавляем его в отсортированный сегмент. Мы не меняем местами промежуточные элементы. Следовательно, этот алгоритм сортирует массив с минимальным количеством перестановок.

Алгоритм сортировки выбором:

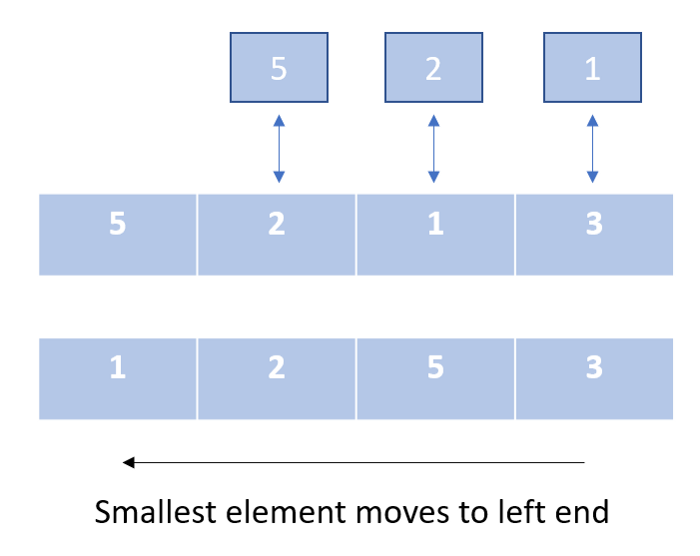
• нерекурсивный;
• может быть как устойчивым, так и неустойчивым;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n²);

def selectionSort(array):
    for i in range(len(array)-1):
        min_idx = i
        for idx in range(i + 1, len(array)-1):
            if array[idx] < array[min_idx]:
                min_idx = idx
        array[i], array[min_idx] = array[min_idx], array[i]
    return array

Сортировка вставками

Подобно алгоритму сортировки выбором, мы делим наш список на две части. Далее мы перебираем неотсортированную часть и вставляем каждый элемент из данного сегмента на его правильное место в отсортированной части списка.

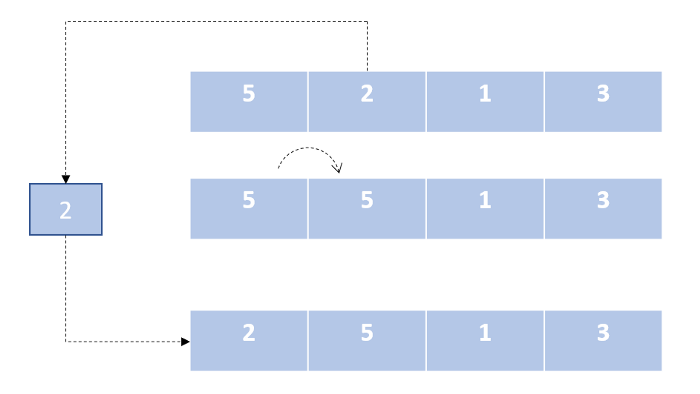
Алгоритм сортировки вставками:

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n²);

def insertionSort(array):
    for i in range(1, len(array)):
        key = array[i]
        j = i-1
        while array[j] > key and j >= 0:
            array[j+1] = array[j]
            j -= 1
        array[j+1] = key
    return array

[python_ad_block]

Сортировка Шелла

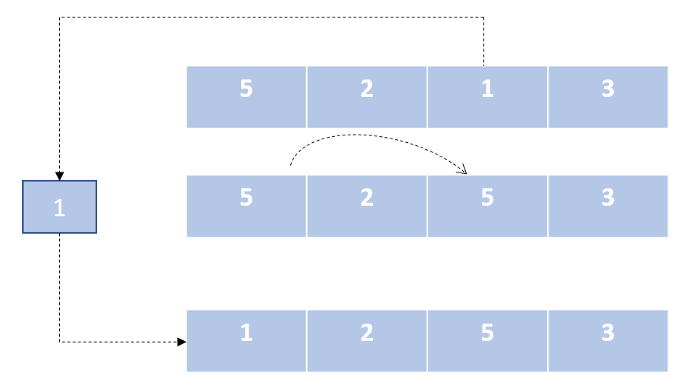
Сортировка Шелла является оптимизированным вариантом сортировки вставками.

Оптимизация достигается путем сравнения не только соседних элементов, но и элементов на определенном расстоянии, которое в течении работы алгоритма уменьшается. На последней итерации это расстояние равно 1. После этого алгоритм становится обычным алгоритмом сортировки вставками, что гарантирует правильный результат сортировки.

Но следует отметить один момент: к тому времени, когда это произойдет, наш массив будет почти отсортирован, поэтому итерации будут выполнятся очень быстро.

Алгоритм сортировки Шелла:

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(n²), но это также зависит от выбора длины интервала;

def shellSort(array):
    n = len(array)
    k = int(math.log2(n))
    interval = 2**k -1
    while interval > 0:
        for i in range(interval, n):
            temp = array[i]
            j = i
            while j >= interval and array[j - interval] > temp:
                array[j] = array[j - interval]
                j -= interval
            array[j] = temp
        k -= 1
        interval = 2**k -1
    return array

Пирамидальная сортировка («сортировка кучей»)

Как и в двух предыдущих алгоритмах, мы создаем два сегмента списка: отсортированный и несортированный.

В данном алгоритме для эффективного нахождения максимального элемента в неотсортированной части списка мы используем структуру данных «куча».

Метод heapify в примере кода использует рекурсию для получения элемента с максимальным значением на вершине.

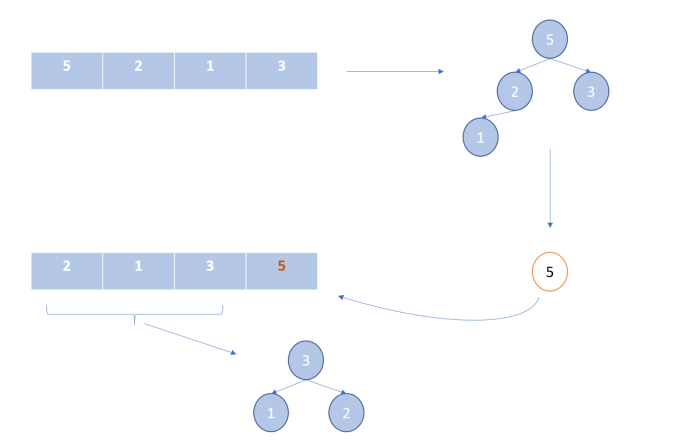
Алгоритм пирамидальной сортировки:

• нерекурсивный;
• неустойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(nlog(n));

def heapify(array, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2
    
    if l < n and array[i] < array[l]:
        largest = l
    if r < n and array[largest] < array[r]:
        largest = r
    
    if largest != i:
        array[i], array[largest] = array[largest], array[i]
        heapify(array, n, largest)
        
def heapSort(array):
    n = len(array)
    for i in range(n//2, -1, -1):
        heapify(array, n, i)
    for i in range(n-1, 0, -1):
        array[i], array[0] = array[0], array[i]
        heapify(array, i, 0)
    return array

Сортировка слиянием

Этот алгоритм работает по принципу «разделяй и властвуй».

Здесь мы делим список ровно пополам и продолжаем это делать, пока в нем не останется только один элемент. Затем мы объединяем уже упорядоченные части нашего списка. Мы продолжаем это делать, пока не получим отсортированный список со всеми элементами несортированного входного списка.

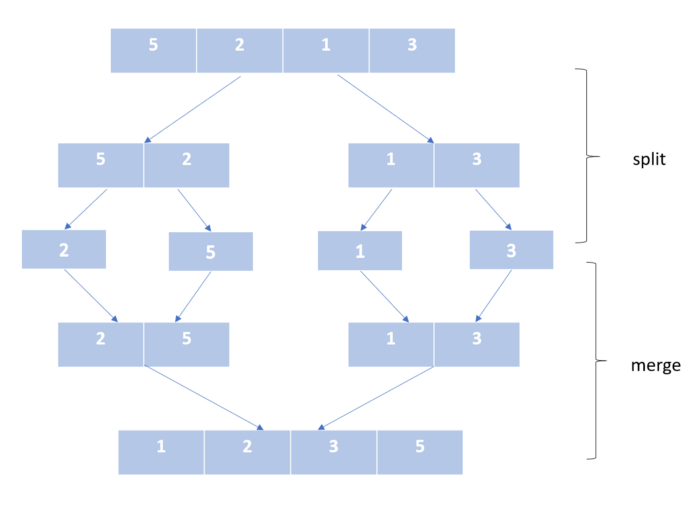
Алгоритм сортировки слиянием:

• рекурсивный;
• устойчивый;
• требует дополнительной памяти;
• имеет сложность O(nlog(n));

def mergeSort(nums):
    if len(nums)==1:
        return nums
    mid = (len(nums)-1) // 2
    lst1 = mergeSort(nums[:mid+1])
    lst2 = mergeSort(nums[mid+1:])
    result = merge(lst1, lst2)
    return result
def merge(lst1, lst2):
    lst = []
    i = 0
    j = 0
    while(i<=len(lst1)-1 and j<=len(lst2)-1):
        if lst1[i]<lst2[j]:
            lst.append(lst1[i])
            i+=1
        else:
            lst.append(lst2[j])
            j+=1
    if i>len(lst1)-1:
        while(j<=len(lst2)-1):
            lst.append(lst2[j])
            j+=1
    else:
        while(i<=len(lst1)-1):
            lst.append(lst1[i])
            i+=1
    return lst

Быстрая сортировка

В этом алгоритме мы разбиваем список при помощи опорного элемента, сортируя значения вокруг него.

В нашей реализации мы выбрали опорным элементом последний элемент массива. Наилучшая производительность достигается тогда, когда опорный элемент делит список примерно пополам.

Алгоритм быстрой сортировки:

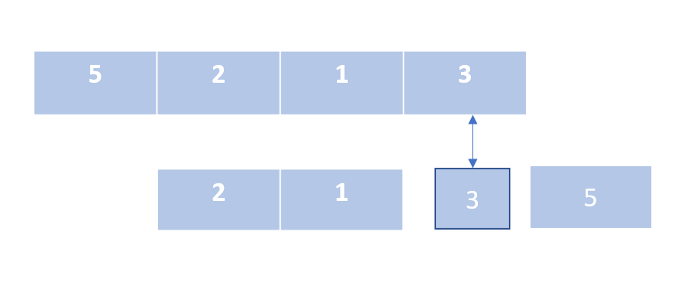
• рекурсивный;
• неустойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place);
• имеет сложность O(nlog(n));

def quickSort(array):
    if len(array)> 1:
        pivot=array.pop()
        grtr_lst, equal_lst, smlr_lst = [], [pivot], []
        for item in array:
            if item == pivot:
                equal_lst.append(item)
            elif item > pivot:
                grtr_lst.append(item)
            else:
                smlr_lst.append(item)
        return (quickSort(smlr_lst) + equal_lst + quickSort(grtr_lst))
    else:
        return array

Сортировка подсчетом

Этот алгоритм не производит сравнение элементов. Для сортировки используются математические свойства целых чисел. Мы подсчитываем вхождения числа в массиве и сохраняем результат во вспомогательном массиве, где индексу соответствует значение ключа.

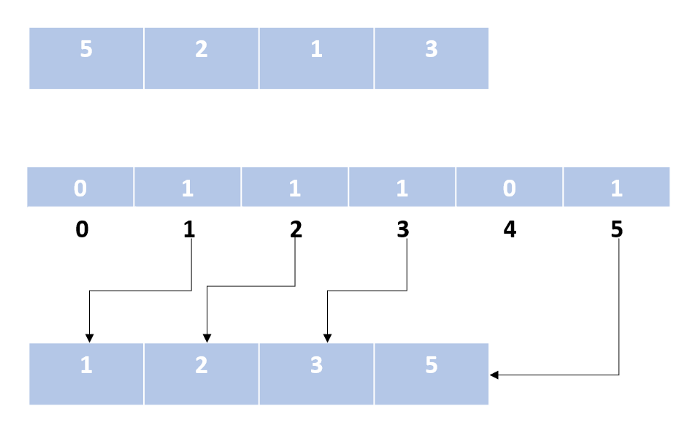
Алгоритм сортировки подсчетом:

• нерекурсивный;
• устойчивый;
• преобразует входные данные без использования вспомогательной структуры данных (in place), но все же требует дополнительной памяти;
• имеет сложность O(n);

def sortArray(self, nums: List[int]) -> List[int]:
    i_lower_bound , upper_bound = min(nums), max(nums)
    lower_bound = i_lower_bound
    if i_lower_bound < 0:
        lb = abs(i_lower_bound)
        nums = [item + lb for item in nums]
        lower_bound , upper_bound = min(nums), max(nums)
    
    counter_nums = [0]*(upper_bound-lower_bound+1)
    for item in nums:
        counter_nums[item-lower_bound] += 1
    pos = 0
    for idx, item in enumerate(counter_nums):
        num = idx + lower_bound
        for i in range(item):
            nums[pos] = num
            pos += 1
    if i_lower_bound < 0:
        lb = abs(i_lower_bound)
        nums = [item - lb for item in nums]
    return nums

Следует также упомянуть поразрядную сортировку, которая использует сортировку подсчетом либо блочную (корзинную) сортировку в качестве подпрограммы. Этот метод сортировки заслуживает отдельной статьи для разбора.

Для удобства соберем весь наш код вместе:

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        # Сортировка пузырьком
        def bubbleSort(array):
            swapped = False
            for i in range(len(array)-1,0,-1):
                for j in range(i):
                    if array[j]>array[j+1]:
                        array[j], array[j+1] = array[j+1], array[j]
                        swapped= True
                if swapped:
                    swapped=False
                else:
                    break
            return array
        
        # Сортировка вставками
        def insertionSort(array):
            for i in range(1, len(array)):
                key = array[i]
                j = i-1
                while array[j] > key and j >= 0:
                    array[j+1] = array[j]
                    j -= 1
                array[j+1] = key
            return array
        
        # Сортировка выбором
        def selectionSort(array):
            for i in range(len(array)-1):
                min_idx = i
                for idx in range(i + 1, len(array)-1):
                    if array[idx] < array[min_idx]:
                        min_idx = idx
                array[i], array[min_idx] = array[min_idx], array[i]
            return array
        
        # Пирамидальная сортировка
        def heapify(array, n, i):
            largest = i
            l = 2 * i + 1
            r = 2 * i + 2

            if l < n and array[i] < array[l]:
                largest = l

            if r < n and array[largest] < array[r]:
                largest = r

            if largest != i:
                array[i], array[largest] = array[largest], array[i]
                heapify(array, n, largest)
                
        def heapSort(array):
            n = len(array)
            for i in range(n//2, -1, -1):
                heapify(array, n, i)
            for i in range(n-1, 0, -1):
                array[i], array[0] = array[0], array[i]
                heapify(array, i, 0)
            return array
        
        # Сортировка слиянием
        def mergeSort(nums):
            if len(nums)==1:
                return nums
            mid = (len(nums)-1) // 2
            lst1 = mergeSort(nums[:mid+1])
            lst2 = mergeSort(nums[mid+1:])
            result = merge(lst1, lst2)
            return result
    
        def merge(lst1, lst2):
            lst = []
            i = 0
            j = 0
            while(i<=len(lst1)-1 and j<=len(lst2)-1):
                if lst1[i]<lst2[j]:
                    lst.append(lst1[i])
                    i+=1
                else:
                    lst.append(lst2[j])
                    j+=1
            if i>len(lst1)-1:
                while(j<=len(lst2)-1):
                    lst.append(lst2[j])
                    j+=1
            else:
                while(i<=len(lst1)-1):
                    lst.append(lst1[i])
                    i+=1
            return lst   
        
        # Быстрая сортировка
        def quickSort(array):
            if len(array)> 1:
                pivot=array.pop()
                grtr_lst, equal_lst, smlr_lst = [], [pivot], []
                for item in array:
                    if item == pivot:
                        equal_lst.append(item)
                    elif item > pivot:
                        grtr_lst.append(item)
                    else:
                        smlr_lst.append(item)
                return (quickSort(smlr_lst) + equal_lst + quickSort(grtr_lst))
            else:
                return array

        # Сортировка Шелла
        def shellSort(array):
            n = len(array)
            interval = n // 2
            while interval > 0:
                for i in range(interval, n):
                    temp = array[i]
                    j = i
                    while j >= interval and array[j - interval] > temp:
                        array[j] = array[j - interval]
                        j -= interval

                    array[j] = temp
                interval //= 2
            return array

        
        #nums = bubbleSort(nums)
        #nums = insertionSort(nums)
        #nums = selectionSort(nums)
        #nums = heapSort(nums)
        #nums = mergeSort(nums)
        #nums = quickSort(nums)

        return nums

Испытав все эти алгоритмы, мы ради любопытства запустили встроенную в Python функцию sorted(). Она показала весьма быстрое время в 152 мс. В данной функции используется алгоритм Timsort, который сочетает в себе сортировку слиянием и сортировку вставками. Реализация данного алгоритма также может быть рассмотрена в отдельной статье.

Мы нашли потрясающий плейлист, в котором алгоритмы сортировки демонстрируются при помощи народного танца. Посмотрите это видео, оно того стоит!

В нашем небольшом исследовании мы изучили различные алгоритмы сортировки и определили время их выполнения, а также их потребности в памяти. Теперь мы понимаем, что значит время выполнения, стабильность алгоритма и используемая память. Чтобы выбрать подходящий алгоритм, мы должны оценивать эти параметры. Также, для создания более эффективных решений, типа Timsort, мы можем комбинировать наши базовые алгоритмы.

Счастливой вам сортировки!

Перевод статьи «Sorting Algorithms — With Python».