Задача, старая как мир. Есть список вещей, который нужно отсортировать. Как это сделать?
Ну, самый интуитивный вариант — взять список, разделить его пополам, затем еще пополам и еще, пока у вас не окажется куча списков с длиной, равной единице. После этого нужно выстроить элементы в пары, располагая их в правильном порядке, а затем соединять эти пары вместе, образуя все большие упорядоченные группы, до тех пор, пока не получите целый отсортированный список. Вам тоже именно это сразу в голову пришло?
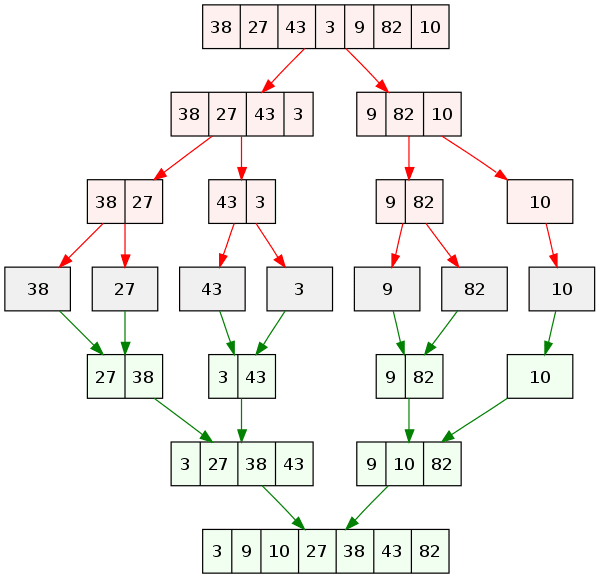
Ну ладно, может, это действительно не самое интуитивное решение, но мы избавим вас от утомительного прохождения сортировки пузырьком или случайной сортировки (тут впору вздрогнуть) и сразу перейдем к объяснению сортировки слиянием. Единственное, что вам нужно знать, это что сортировка слиянием по сравнению с другими алгоритмами довольно эффективна. Временная сложность этого алгоритма, как вы можете догадаться по подходу «разделим пополам», — O(N log N).
Итак, давайте начнем. Создадим функцию merge_sort(), которая будет принимать список. Для наших целей мы назовем этот список nums (т. е. «числа»), но тот же метод будет работать со списком любых сортируемых типов, например, со списком строк.
def merge_sort(nums):
pass
Наш первый шаг — разделить список надвое. Мы будем использовать целочисленное деление, чтобы в итоге получить целый индекс (а то вдруг у нас в списке нечетное количество элементов). Затем мы создадим два меньших списка, left и right. Для этого мы используем очень удобную нотацию Python для подсписков.
Погодите, а если длина списка будет 0 или 1? Мы же тогда не сможем разделить его пополам! Чтобы учесть такую возможность, мы обернем весь наш метод в if-предложение. Таким образом весь этот код будет работать только если длина списка больше 1.
def merge_sort(nums):
if len(nums) >1:
mid = len(nums)//2
left = nums[:mid]
right = nums[mid:]
Что мы делаем дальше? Все просто! Мы отсортируем обе половины, вызывая для них merge_sort().
def merge_sort(nums):
if len(nums) >1:
mid = len(nums)//2
left = nums[:mid]
right = nums[mid:]
merge_sort(left)
merge_sort(right)
Но погодите, это еще не все. Пока что мы просто последовательно делили наши списки пополам, пока не получили кучу маленьких списков с длиной, равной 1. Например, если бы у нас был список [4, 2, 1, 3], он был бы разделен на [4, 2] и [1, 3], а затем на [4], [2], [1] и [3] (каждый из этих списков имеет длину, равную 1).
Что дальше? Подсказка кроется в названии алгоритма сортировки. Дальше будет слияние списков.
Здесь нужно быть внимательным. Нам нужно отслеживать три индекса. Назовем их i, j и k. Вот что они будут представлять:
i— индекс в спискеleft,j— индекс в спискеright,k— индекс в исходном спискеnums, в который в конечном итоге нужно вставить все числа по порядку.
Для начала давайте зададим им всем значение 0.
i = j = k = 0
После этого мы будем перебирать и левый, и правый список, сравнивая каждый элемент. Пройти списки необходимо только один раз, потому что left и right уже отсортированы. Нам нужно только соединить их.
Если число из списка left меньше, чем число из списка right, мы вставляем его в nums на позицию k, после чего увеличиваем индекс i на единицу. Если число из списка right меньше или равно числу из списка left, тогда оно отправляется в nums, а мы увеличиваем на единицу индекс j. Наконец, после добавления любого из чисел в список nums, мы увеличиваем на единицу индекс k.
while i < len(left) and j < len(right):
if left[i] < right[j]:
nums[k] = left[i]
i+=1
else:
nums[k] = right[j]
j+=1
k+=1
Но нужно еще кое-что сделать. Мы написали while i < len(left) and j < len(right), то есть, если эти условия выполняются, цикл прерывается. Но что, если мы дойдем до конца списка left, а в списке right еще останутся элементы? На этот случай нам нужно сделать еще один цикл while. В этом цикле мы будем перебирать остаток элементов в списке right и добавлять их в список nums. То же самое мы сделаем и для списка left.
while j < len(right):
nums[k] = right[j]
j+=1
k+=1
while i < len(left):
nums[k] = left[i]
i+=1
k+=1
Вот и все! Что касается слияния, мы начали со списков [4], [2], [1] и [3]. Эти списки соединились в [2, 4] и [1, 3], а затем образовали [1, 2, 3, 4].
Вот наш полный код. Заметьте, что весь метод по сути лежит в самом первом блоке if.
def merge_sort(nums):
if len(nums) > 1:
mid = len(nums)//2
left = nums[:mid]
right = nums[mid:]
merge_sort(left)
merge_sort(right)
i = j = k = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
nums[k] = left[i]
i+=1
else:
nums[k] = right[j]
j+=1
k+=1
while i < len(left):
nums[k] = left[i]
i+=1
k+=1
while j < len(right):
nums[k] = right[j]
j+=1
k+=1
Проверка
Давайте отсортируем какие-нибудь числа. Создадим список чисел и вызовем для него merge_sort(). Обратите внимание, что мы выводим в результате тот же список nums, потому что наш метод ничего не возвращает, а лишь изменяет исходный список.
nums = [5, 2, 3, 6, 84, 9, 8] merge_sort(nums) print(nums)
В результате вы должны получить отсортированный список — [2, 3, 5, 6, 8, 9, 84]. Как уже говорилось, это сработает и со строками. Если передать этому методу список ['banana', 'apple', 'grape', 'orange'], он будет отсортирован в алфавитном порядке: ['apple', 'banana', 'grape', 'orange'].
Метод .sort() в Python работает сходным образом, это тоже алгоритм из серии «разделяй и властвуй», да и временная сложность у него приблизительно такая же. В общем, нет никаких причин, по которым вам стоило бы реализовывать сортировку слиянием… если не вспоминать о технических собеседованиях, конечно. Но теперь-то вы будете готовы к таким заданиям!

