В этой статье мы подробно разберем, как создать последовательность Фибоначчи. Решение данной задачи мы покажем с использованием трех разных методов. Рассмотрим мемоизацию, рекурсию и цикл for в Python.
Как вы, вероятно, знаете, последовательность Фибоначчи образуется следующим образом. Мы складываем первое и второе число, 0 и 1, чтобы получить третье число в последовательности (0 + 1 = 1). Затем мы складываем второе и третье число, чтобы получить 4-е число в последовательности (1 + 1 = 2). И так проделываем для каждого последующего числа Фибоначчи.
Код, который мы будем рассматривать, вы можете писать в Jupyter, Colab или любой IDE или текстовом редакторе, который вам удобен.
Вычисление n-го члена последовательности Фибоначчи с помощью цикла for
Напишем базовую программу, используя цикл for. Логика последовательности проста, мы уже обсудили ее выше.
Временная сложность решения с помощью цикла for — O(n), а пространственная сложность – O(1) или константа. Правда, на самом деле все несколько сложнее.
«Если ваше число меньше, чем 94, и вы используете 64-битное число, тогда алгоритм ведет себя, как имеющий линейную сложность. Но для N > 94 он начинает вести себя, как алгоритм с квадратичной сложностью», — из ответа Майкла Векслера на сайте Quora.
def fib_for(n):
n1 = 0
n2 = 1
if n <= 0:
return 'Введите число больше 0'
elif n == 1:
return n1
elif n == 2:
return n2
else:
for i in range(2, n):
n1, n2 = n2, n1 + n2
return n2
Запустим этот код с помощью модуля Python %timeit. Это позволит замерить время выполнения, избежав ряда распространенных ловушек.

Для того, чтобы высчитать 10-е число Фибоначчи, потребовалось по 675 наносекунд на каждую итерацию цикла.
Вычисление n-го члена последовательности Фибоначчи с помощью рекурсии
Теперь давайте реализуем последовательность Фибоначчи с помощью рекурсии. Рекурсивные функции вызывают себя повторно, пока не достигнут базового случая. Таким образом, рекурсия создает древовидную структуру.
Если мы возьмем первые 5 чисел Фибоначчи, то в результате рекурсии получится вот такое дерево.
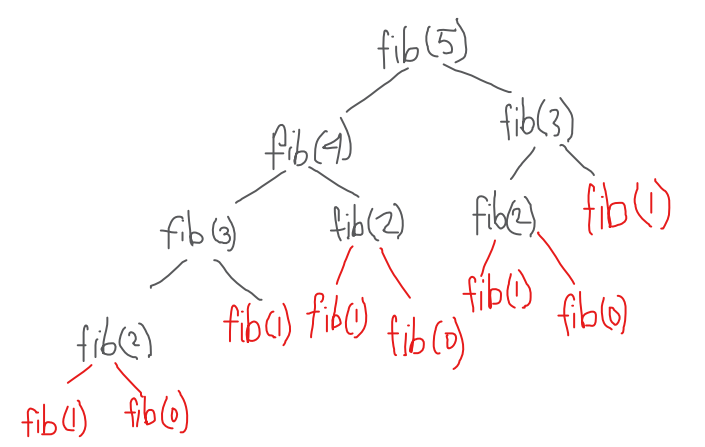
Пространственная сложность в данном случае — O(n), а временная сложность — O(2n). Так происходит, потому что у корневого узла есть 2 дочерних узла (fib(4) и fib(3)) и 4 внука. И, как видите, у каждого узла есть 2 дочерних элемента. Кроме того, вы могли заметить, что правое поддерево меньше, чем левое. Так что, на самом деле время выполнения составляет примерно O(1,6n).
Базовый случай: Fibonacci(2) = Fib(1) + Fib(0) = 1 + 0 = 1
def fib_recursion(n):
if n <= 0:
return 'Введите число больше 0'
elif n == 1:
return 0
elif n == 2:
return 1
else:
return fib_recursion(n - 1) + fib_recursion(n - 2)
Вычисление n-го члена последовательности Фибоначчи при помощи рекурсии определенно быстрее, чем с помощью цикла for.
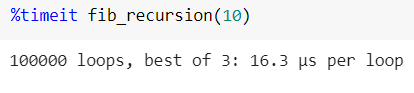
Вычисление n-го члена последовательности Фибоначчи с использованием мемоизации
Мемоизация – это метод, который может значительно улучшить производительность рекурсивной функции за счет уменьшения вычислительных затрат. Он сохраняет результаты дорогостоящих вызовов функций в массиве или словаре и при вызове с такими же входными данными возвращает кэшированные результаты.
Давайте ещё раз посмотрим на приведенное выше дерево. Легко заметить, что некоторые входные данные пересчитываются при каждом обращении к ним.
def Fib_memoisation(n, memo):
if n <= 0:
return 'Введите число больше 0'
elif n == 1:
return 0
elif n == 2:
return 1
else:
if n not in memo:
memo[n] = Fib_memoisation(n - 1, memo) + Fib_memoisation(n - 2, memo)
return memo[n]
Временная сложность — O(n * log10n).
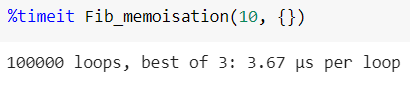
Что лучше: рекурсия, цикл for или мемоизация?
Нельзя сказать, что какая-то из этих техник однозначно лучше других. Вам просто нужно знать, в каких случаях какая из них будет наиболее подходящей и эффективной. Это, конечно же, зависит от ваших требований.
Итерация с помощью цикла for будет быстрее, чем рекурсия, потому что рекурсия должна иметь дело с фреймом рекурсивного стека вызовов. Однако, если рекурсия написана на языке, который оптимизирует «хвостовой» вызов, это устраняет излишние расходы, и тогда рекурсия сравнима с циклом for.
Наконец, мемоизация лучше, когда нужно иметь дело только с некоторыми более мелкими подзадачами, а не решать их все.
Таким образом, каждый из разобранных нами в этой статье методов по-своему хорош. Стоит помнить о существовании и особенностях каждого из них и выбирать наиболее оптимальный под вашу задачу.

