Обход двоичного дерева на Python (примеры кода)

Да, двоичные деревья — не самая любимая тема программистов. Это одна из тех старых концепций, о целесообразности изучения которых постоянно ведутся споры. В работе вам довольно редко придется реализовывать двоичные деревья и обходить их, так зачем же уделять им так много внимания на технических собеседованиях?

Сегодня мы не будем переворачивать двоичное дерево (ффухх!), но рассмотрим пару методов его обхода. К концу статьи вы поймете, что двоичные деревья не так страшны, как кажется.

Что такое двоичное дерево?

Недавно мы разбирали реализацию связных списков на Python. Каждый такой список состоит из некоторого количества узлов, указывающих на другие узлы. А если бы узел мог указывать не на один другой узел, а на большее их число? Вот это и есть деревья. В них каждый родительский узел может иметь несколько узлов-потомков. Если у каждого узла максимум два узла-потомка (левый и правый), такое дерево называется двоичным (бинарным).

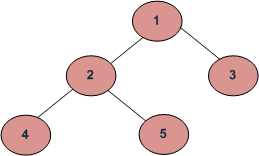
Схема двоичного дерева с 5 узлами, корень - 1.

В приведенном выше примере «корень» дерева, т. е. самый верхний узел, имеет значение 1. Его потомки — 2 и 3. Узлы 3, 4 и 5 называют «листьями»: у них нет узлов-потомков.

Строим двоичное дерево на Python

Как построить дерево на Python? Реализация будет похожей на наш класс Node в реализации связного списка. В этом случае мы назовем класс TreeNode.

class TreeNode:
    pass

Определим метод __init__(). Как всегда, он принимает self. Также мы передаем в него значение, которое будет храниться в узле.

class TreeNode:
    def __init__(self, value):

Установим значение узла, а затем определим левый и правый указатель (для начала поставим им значение None).

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

И… все! Что, думали, что деревья куда сложнее? Если речь идет о двоичном дереве, единственное, что его отличает от связного списка, это то, что вместо next у нас тут есть left и right.

Давайте построим дерево, которое изображено на схеме в начале статьи. Верхний узел имеет значение 1. Далее мы устанавливаем левые и правые узлы, пока не получим желаемое дерево.

tree = TreeNode(1)
tree.left = TreeNode(2)
tree.right = TreeNode(3)
tree.left.left = TreeNode(4)
tree.left.right = TreeNode(5)

Обход двоичного дерева

Итак, вы построили дерево и теперь вам, вероятно, любопытно, как же его увидеть. Нет никакой команды, которая позволила бы вывести на экран дерево целиком, тем не менее мы можем обойти его, посетив каждый узел. Но в каком порядке выводить узлы?

Самые простые в реализации обходы дерева — прямой (Pre-Order), обратный (Post-Order) и центрированный (In-Order). Вы также можете услышать такие термины, как поиск в ширину и поиск в глубину, но их реализация сложнее, ее мы рассмотрим как-нибудь потом.

Итак, что из себя представляют три варианта обхода, указанные выше? Давайте еще раз посмотрим на наше дерево.

При прямом обходе мы посещаем родительские узлы до посещения узлов-потомков. В случае с нашим деревом мы будем обходить узлы в таком порядке: 1, 2, 4, 5, 3.

Обратный обход двоичного дерева — это когда вы сначала посещаете узлы-потомки, а затем — их родительские узлы. В нашем случае порядок посещения узлов при обратном обходе будет таким: 4, 5, 2, 3, 1.

При центрированном обходе мы посещаем все узлы слева направо. Центрированный обход нашего дерева — это посещение узлов 4, 2, 5, 1, 3.

Давайте напишем методы обхода для нашего двоичного дерева.

Pre-Order

Начнем с определения метода pre_order(). Наш метод принимает один аргумент — корневой узел (расположенный выше всех).

def pre_order(node):
    pass

Дальше нам нужно проверить, существует ли этот узел. Вы можете возразить, что лучше бы проверить существование потомков этого узла перед их посещением. Но для этого нам пришлось бы написать два if-предложения, а так мы обойдемся одним.

def pre_order(node):
    if node:
        pass

Написать обход просто. Прямой обход — это посещение родительского узла, а затем каждого из его потомков. Мы «посетим» родительский узел, выведя его на экран, а затем «обойдем» детей, вызывая этот метод рекурсивно для каждого узла-потомка.

# Выводит родителя до всех его потомков
def pre_order(node):
    if node:
        print(node.value)
        pre_order(node.left)
        pre_order(node.right)

Просто, правда? Можем протестировать этот код, совершив обход построенного ранее дерева.

 pre_order(tree)

Результат:

Превосходно.

Post-Order

Переходим к обратному обходу. Возможно, вы думаете, что для этого нужно написать еще один метод, но на самом деле нам нужно изменить всего одну строчку в предыдущем.

Вместо «посещения» родительского узла и последующего «обхода» детей, мы сначала «обойдем» детей, а затем «посетим» родительский узел. То есть, мы просто передвинем print на последнюю строку! Не забудьте поменять имя метода на post_order() во всех вызовах.

# Выводит потомков, а затем родителя
def post_order(node):
    if node:
        post_order(node.left)
        post_order(node.right)
        print(node.value)

В выводе мы получим:

Каждый узел-потомок посещен до посещения его родителя.

In-Order

Наконец, напишем метод центрированного обхода. Как нам обойти левый узел, затем родительский, а затем правый? Опять же, нужно переместить предложение print!

# выводит левого потомка, затем родителя, затем правого потомка
def in_order(node):
    if node:
        in_order(node.left)
        print(node.value)
        in_order(node.right)