
Мы уже знаем, что такое двоичное дерево и как его построить. Также мы рассмотрели, что такое поиск в ширину и глубину. Теперь давайте попробуем использовать все эти знания и решить задачу.
Вот задача с LeetCode:
Дан корень двоичного дерева. Проверьте, является ли это дерево зеркальным отражением самого себя (т. е. симметричным относительно своего центра).
Давайте рассмотрим пару примеров.
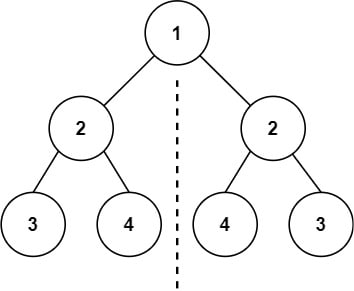
Нам нужно написать функцию для проверки зеркальности дерева. Если в такую функцию передать корневой узел дерева, изображенного на схеме выше, функция должна вернуть True. Значения в левой части дерева зеркально отражают значения в правой.
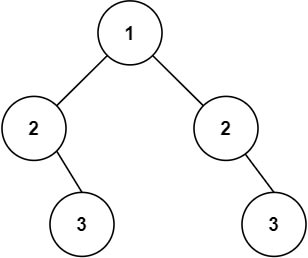

В дереве, изображенном на второй схеме, узлы со значением 3 расположены не зеркально, они не являются отражениями друг друга относительно центра. Поэтому при передаче в нашу функцию корня этого дерева функция должна вернуть False.
1. Стратегия решения
Как обычно при решении задач на тему двоичных деревьев, первое, что нужно решить, это будем мы обходить дерево в ширину или в глубину.
На первый взгляд кажется, что имеет смысл обходить дерево в ширину и проверять, одинаковы ли узлы, находящиеся на одном уровне в двух половинках дерева. Но когда мы дойдем до третьего уровня с его узлами 3, 4, 4, 3, задача внезапно усложнится. Не лучше ли разделить дерево на две половины и совершить обход в глубину по каждой из них?
Давайте еще раз посмотрим на первый пример:



Если обойти в глубину левую половину дерева, узлы будут прочитаны в порядке 2, 3, 4. Одновременно мы можем совершить обход в глубину правой половины дерева и вывести те же узлы 2, 3, 4. Из этого мы сможем сделать вывод, что дерево симметрично.
2. Начальная подготовка
Первое, что нам нужно, это написать класс TreeNode. Он будет принимать data (значение, которое мы хотим сохранить в узле), и указатели left и right, инициализированные в None.
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
Дальше нам нужно определить наш метод. Он будет принимать одно значение: корневой узел дерева.
def is_mirror(root):
pass
Как вы помните, мы собирались разрезать дерево на две половины и проверять узлы в каждой половине. Мы это сделаем при помощи вспомогательного рекурсивного метода check_halves. Этот метод принимает левый и правый узел (в начале — root.left и root.right).
def is_mirror(root):
return check_halves(root.left, root.right)
3. Обход
Как и в большинстве обходов деревьев, мы используем рекурсию. Начнем с определения нашего вспомогательного метода, принимающего left и right.
def check_halves(left, right):
Каким будет наш базовый случай? Самым простым примером будет дерево с единственным узлом (корневым). Значения обеих его половин будет None. В этом случае мы вернем True.
def check_halves(left, right):
if not left and not right:
return True
Что дальше? Нам нужно проверить, есть ли одновременно левый и правый узел, а также — совпадают ли их значения. Это можно поместить в одно if-предложение, но для ясности лучше разделить.
def check_halves(left, right):
if not left and not right:
return True
if left and right:
if left.data == right.data:
А дальше мы входим в рекурсию! Мы будем делать обход в глубину левой и правой половинки дерева.
left_half = check_halves(left.left, right.right) right_half = check_halves(left.right, right.left)
Затем нам нужно проверить, обе ли половины — True. Это можно сделать при помощи оператора and.
return left_half and right_half
Наконец, мы вернем False, если предыдущее if-условие не соблюдено. Целиком наш вспомогательный метод выглядит следующим образом:
def check_halves(left, right):
if not left and not right:
return True
if left and right:
if left.data == right.data:
left_half = check_halves(left.left, right.right)
right_half = check_halves(left.right, right.left)
return left_half and right_half
return False
4. Проверяем
При помощи следующего кода построим дерево с первой схемы.
tree1 = TreeNode(1) tree1.left = TreeNode(2) tree1.right = TreeNode(2) tree1.left.left = TreeNode(3) tree1.right.right = TreeNode(3) tree1.left.right = TreeNode(4) tree1.right.left = TreeNode(4)
Теперь нам нужно вызвать print(is_mirror(tree1)). Функция возвращает True. Ура!
Давайте попробуем применить эту функцию для несимметричного дерева, такого, как на второй схеме. Два узла этого дерева, имеющие значение 3, расположены не зеркально.
tree2 = TreeNode(1) tree2.left = TreeNode(2) tree2.right = TreeNode(2) tree2.left.left = TreeNode(3) tree2.right.left = TreeNode(3)
print(is_mirror(tree2)) выведет False. То же самое случится, если мы поменяем какие-нибудь значения в первом дереве, чтобы оно стало несимметричным.

