Предыдущая статья — Глубокое обучение и нейронные сети с Python и Pytorch. Часть III: построение нашей нейронной сети.
В предыдущей статье мы создали нашу нейронную сеть. В этой, четвертой статье из серии «Глубокое обучение и нейронные сети с Python и Pytorch» мы фактически обучим эту нейронную сеть, а также узнаем, как перебирать наши данные, переходить к модели, вычислять функцию потерь, а затем выполнять алгоритм обратного распространения ошибки, чтобы постепенно подогнать нашу модель к данным.
К настоящему моменту наш код имеет следующий вид:
import torch
import torchvision
from torchvision import transforms, datasets
import torch.nn as nn
import torch.nn.functional as F
train = datasets.MNIST('', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor()
]))
test = datasets.MNIST('', train=False, download=True,
transform=transforms.Compose([
transforms.ToTensor()
]))
trainset = torch.utils.data.DataLoader(train, batch_size=10, shuffle=True)
testset = torch.utils.data.DataLoader(test, batch_size=10, shuffle=False)
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(28*28, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = self.fc4(x)
return F.log_softmax(x, dim=1)
net = Net()
print(net)
Net(
(fc1): Linear(in_features=784, out_features=64, bias=True)
(fc2): Linear(in_features=64, out_features=64, bias=True)
(fc3): Linear(in_features=64, out_features=64, bias=True)
(fc4): Linear(in_features=64, out_features=10, bias=True)
)
К счастью для нас, используемые нами данные из фреймворка Pytorch на самом деле являются красивыми забавными объектами, которые не нуждаются в дополнительной предобработке. Они уже разбиты на батчи и нам надо только их проитерировать. Также нам необходимо вычислить функцию потерь и задать функцию оптимизации:
import torch.optim as optim loss_function = nn.CrossEntropyLoss() optimizer = optim.Adam(net.parameters(), lr=0.001)
Функция потерь (loss_function) вычисляет, насколько далеко результаты нашей классификации отошли от реальности. Как люди, мы склонны думать о вещах в терминах «правильно» или «неправильно». С точки зрения нейронной сети и, возможно, некоторых людей тоже, наша точность на самом деле является своего рода шкалой.
Например, представьте, что вы в чем-то абсолютно уверены, но при этом вы ошибаетесь. И другая ситуация, когда вы не уверены, так это или нет, но тоже ошибаетесь. С точки зрения принятия решений и результата разницы нет. Но с точки зрения вашего обучения она есть.
С точки зрения машинного обучения, когда происходит настройка множества мелких параметров для постепенного приближения к цели, то, насколько все неверно, тоже определенно имеет значение.
Для этого мы используем функцию потерь, которая является мерой того, насколько нейронная сеть далека от правильного результата. Существует несколько способов определять эту величину. Один из популярных способов это использование среднеквадратичной ошибки. Но в нашей задаче используются скалярные классы и для нас это не лучший вариант.
В общем, у вас может быть два типа выходных классов (в задачах классификации — прим. переводчика). Один представляет собой просто скалярные значения, а другой является так называемым горячим вектором (one-hot vector, также иногда переводится как бинарный вектор — прим. переводчика).
В нашем случае, например, число ноль может классифицироваться как 0 или [1, 0, 0, 0, 0, 0, 0 ,0 ,0 ,0].
[1, 0, 0, 0, 0, 0, 0 ,0 ,0 ,0] — это горячий (бинарный) массив, в котором буквально только один элемент равен 1, а остальные 0. Индекс данного массива и будет результатом классификации.
Так, для числа 3 данный массив или вектор будет иметь следующий вид: [0, 0, 0, 1, 0, 0, 0 ,0 ,0 ,0].
Мы, как правило, используем горячий (бинарный) массив, но он определяет скалярные данные: 0, 1, 2, 3… и так далее.
Функцию потерь нужно выбирать в зависимости от того, какой вид имеет ваша целевая переменная.
Для горячего (бинарного) массива более предпочтительна среднеквадратичная ошибка. А для скалярной классификации мы будем использовать кросс-энтропию.
Далее, перейдем к функции оптимизации (оптимайзеру). Это то, что регулирует изменяемые параметры нашей модели, а именно веса, чтобы они постепенно, с течением времени, приходили в соответствие нашим данным.
Мы будем использовать алгоритм под названием Adam (Adaptive Momentum). Это стандартный и широко распространенный оптимайзер. Недавно появился еще улучшенный Adam (rectified Adam) и он активно набирает обороты. Нам еще не довелось попробовать его на реальных проектах и мы не уверены, что его можно просто импортировать из Pytorch, но имейте его в виду!
Есть еще один параметр, который нам необходимо задать. Он называется скорость оптимизации или обучения, lr (learning rate). Для начала положим его равным 0.001 или 1e-3. Скорость обучения определяет величину изменений, которую оптимайзер может внести за один раз. Таким образом, чем больше lr, тем быстрее модель будет обучаться, но вы также можете обнаружить, что шаги, которые вы позволяете оптимайзеру делать, на самом деле слишком велики, и алгоритм не улучшается, а просто застревает на месте, прыгая туда-сюда. Если взять данный параметр слишком маленьким, то модель будет заметно дольше обучаться и точно так же может застревать на месте.
Представьте себе этот параметр в виде количества шагов, которые оптимайзеру нужно сделать, чтобы достичь подножия горы, где путь вниз не обязательно является прямым. Вот несколько прекрасных изображений, которые помогут объяснить параметр «скорость обучения»:
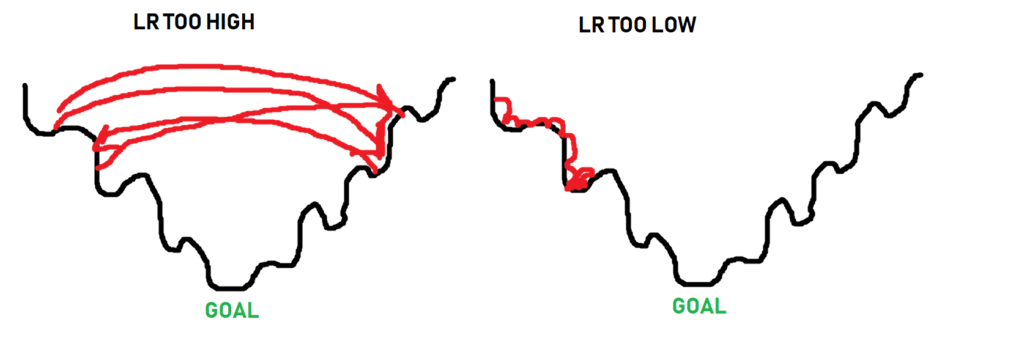
Черная линия — это путь к глобальному минимуму кривой оптимизации. Когда дело доходит до оптимизации, иногда нужно увеличивать скорость обучения, чтобы выйти за пределы некоего локального минимума. Оптимайзер не знает, где находится нужное место, он просто делает шаги и проверяет, оно это или нет. Таким образом, как вы можете видеть на изображении, если шаги слишком большие, до нижних точек никак не добраться. Если шаги слишком малы (слишком мала скорость обучения), алгоритм также может застрять задолго до того, как достигнет дна. Наша цель — получить что-то типа этого:
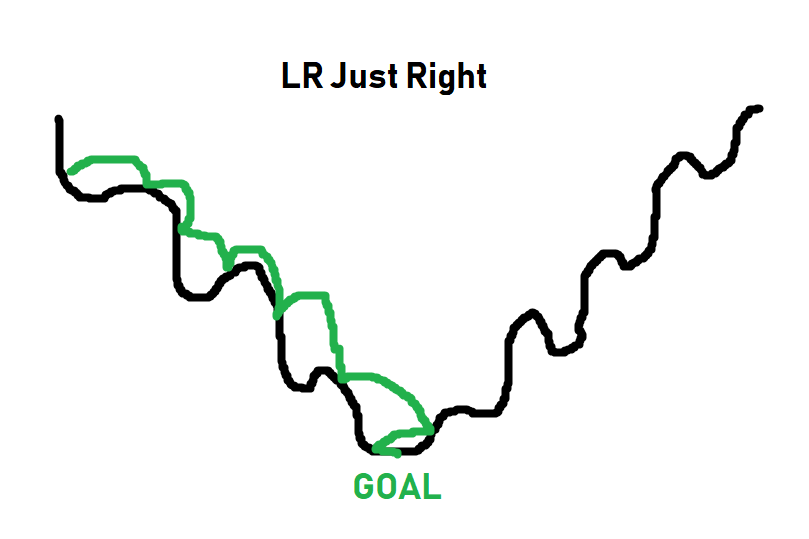
Для простых задач lr = 0.001 обычно отлично подходит. Для более сложных задач нужно определить скорость обучения вместе с так называемым затуханием (decay). Обычно вы стартуете со скоростью обучения равной 0.001 или 0.01, а затем она с каждым разом начинает становиться все меньше и меньше. Идея состоит в том, чтобы сначала быстро обучаться, а потом попытаться достичь наилучшего результата.
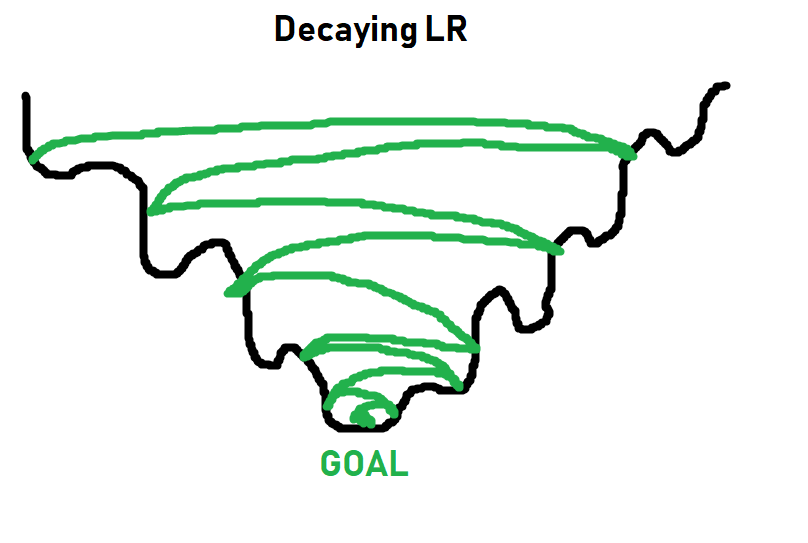
Более подробно о скорости обучения и затухании мы поговорим позже. На данный момент 0,001 будет работать нормально, и вам просто нужно думать о скорости обучения следующим образом: как быстро мы должны заставить этот оптимайзер работать.
Теперь мы можем начать перебирать наши данные. В общем случае вы сделаете точно больше чем один проход по нашим тренировочным данным.
Каждый полный проход по данным называется эпохой (epoch). В общем случае вам потребуется где-то от 3 до 10 эпох, но какого-то жесткого правила тут нет.
Если будет слишком мало эпох, ваша модель не обучится всему, чему могла бы обучиться.
Если их будет слишком много, она переобучится, то есть запомнит все тренировочные данные, а за их пределами работать нормально не сможет.
Давайте для начала начнем с трех эпох. То есть мы сделаем цикл для трех эпох и внутри него будем осуществлять проход по всем данным. Код будет иметь примерно такой вид:
for epoch in range(3): # три полных прохода по нашим данным
for data in trainset: # `data` это батч наших данных
X, y = data # X это батч свойств, y это батч целевых переменных.
net.zero_grad() # устанавливаем значение градиента в 0 перед вычислением функции потерь. Вам следует делать это на каждом шаге.
output = net(X.view(-1,784)) # передаем выпрямленный батч
loss = F.nll_loss(output, y) # вычисляем функцию потерь
loss.backward() # передаем это значение назад по сети
optimizer.step() # пытаемся оптимизировать значение весов исходя из потерь и градиента
print(loss) # выводим на экран значение функции потерь. Мы надеемся, что оно убывает!
tensor(0.4054, grad_fn=<NllLossBackward>) tensor(0.4121, grad_fn=<NllLossBackward>) tensor(0.0206, grad_fn=<NllLossBackward>)
Каждая строка в коде прокомментирована, но концепция градиентов может быть не вполне понятна. Каждый раз, когда мы проходим по нашей нейронной сети и получаем результат, мы сравниваем его с правильным результатом. Благодаря этому мы можем вычислить градиенты для каждого параметра, который наш оптимайзер (Adam, SGD … и т.д.) будет использовать в качестве информации для обновления весов.
Вот почему важно выполнять функцию net.zero_grad (), обнуляющую градиенты, для каждого шага, иначе эти градиенты будут складываться на каждом проходе, и тогда мы будем повторно оптимизировать для предыдущих градиентов, для которых мы уже это сделали.
Итак, что же мы делаем для каждой эпохи и для каждого батча?
- Берем свойства (Х) и целевые переменные (y) из текущего батча.
- Обнуляем градиенты.
- Передаем эти данные вперед через нейронную сеть.
- Вычисляем функцию потерь.
- Изменяем веса в сети в надежде уменьшить значение функции потерь.
В процессе итераций мы вычисляем функцию потерь, которая является очень важной метрикой. Но нам надо позаботиться и о точности. Как же нам это сделать? Для этого нам всего лишь нужно пройтись по тестовому набору данных и сравнить полученные результаты со значениями целевой переменной.
correct = 0 total = 0
with torch.no_grad():
for data in testset:
X, y = data
output = net(X.view(-1,784))
#print(output)
for idx, i in enumerate(output):
#print(torch.argmax(i), y[idx])
if torch.argmax(i) == y[idx]:
correct += 1
total += 1
print("Accuracy: ", round(correct/total, 3))
Accuracy: 0.968
Можно сказать, что у нас тут все хорошо.
import matplotlib.pyplot as plt
plt.imshow(X[0].view(28,28)) plt.show()

print(torch.argmax(net(X[0].view(-1,784))[0]))
tensor(7)
Результат выше может быть немного непонятным, поэтому давайте его разберем поподробнее.
a_featureset = X[0] reshaped_for_network = a_featureset.view(-1,784) # 784 = 28*28 наше разрешение. output = net(reshaped_for_network) #результат будет списком предсказаний нашей сети. first_pred = output[0] print(first_pred)
tensor([-1.9319e+01, -1.1778e+01, -1.0212e+01, -7.2939e+00, -1.8264e+01,
-1.3537e+01, -3.7725e+01, -7.3906e-04, -1.1903e+01, -1.1936e+01],
grad_fn=<SelectBackward>)
Какой индекс у наибольшего элемента? Для определения этого воспользуемся функцией argmax().
biggest_index = torch.argmax(first_pred) print(biggest_index)
tensor(7)
С этим примером мы могли бы сделать гораздо больше, но я думаю, что нам лучше двигаться дальше.
Самостоятельно вы можете подумать над построением графика изменения функции потерь и точности с течением времени. Также можете попробовать нарисовать свою собственную цифру и проверить, узнает ли ее сеть.
Каким бы забавным и простым ни было использование готового набора данных, одна из первых вещей, которые вы действительно захотите предпринять после изучения глубокого обучения, это сделать то, что вам лично интересно. Зачастую это означает, что ваш собственный набор данных будет совершенно неподготовленным, в отличие от данного примера.
В следующих частях мы планируем разобрать сверточные нейронные сети и классификацию изображений кошек и собак. Также затронем и некоторые другие темы, например отслеживание обучения с течением времени.
Следующая часть — Глубокое обучение и нейронные сети с Python и Pytorch. Часть V: сверточные нейронные сети.

