Предыдущая статья — Глубокое обучение и нейронные сети с Python и Pytorch. Часть VII: запускаем обучение на GPU.
Добро пожаловать в восьмую часть серии статей о глубоком обучении при помощи фреймворка Pytorch. В этой статье мы расскажем, как проводить анализ нашей модели (по крайней мере, на базовом уровне). Также мы еще раз подробно пройдем по всему циклу обучения и кода.
Один из основных наших вопросов на данный момент — сколько эпох обучения мы должны произвести? Как мы узнаем, когда надо остановить обучение?
Мы определили, что наша модель действительно обучается, но как нам понять, хуже она или лучше какой-нибудь другой модели, которую мы можем рассмотреть?
Имея большие наборы данных и модели, обучение которых может занимать дни, недели или месяцы, мы хотим знать, как оценивать их за более короткие периоды времени, чтобы определить, следует ли нам продолжать обучение.
Для начала нам нужно хотя бы научиться вычислять точность и потери на уровне эпох (или даже более детально).
Мы хотим вычислять точность двух видов:
- Точность внутри выборки (точность обучения): это точность, посчитанная на данных, которые мы фактически передали в нашу модель. Это данные, на которых мы учимся.
- Точность вне выборки (тестовая точность): это точность, посчитанная на данных, которые мы заранее отделили и которые наша модель никогда не видела.
В целом, мы ожидаем, что точность внутри выборки будет выше, чем точность вне выборки, но при этом мы хотим отслеживать разницу между ними. Дельта в 5-10% вполне нормальна, но ее существенный рост обычно сигнализирует нам о том, что наша модель начинает переобучаться (нейронная сеть просто запоминает данные и меняет веса, чтобы подстроиться именно под эти данные; соответственно, общее понимание данных и их закономерностей от этого страдает).
Также можно отслеживать и функции потерь. Вы часто увидите, что обе функции потерь снижаются до определенной точки, а затем начинают образовывать дугу и изгибаться обратно вверх. Обычно это признак того, что вы получили максимум от обучения модели.
Скорее всего, мы сможем увидеть это на практике с нашим текущим набором данных, поэтому давайте начнем работать над кодом, чтобы разобраться со всем этим. Наш код на данный момент имеет следующий вид:
import os
import cv2
import numpy as np
from tqdm import tqdm
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
REBUILD_DATA = False # set to true to one once, then back to false unless you want to change something in your training data.
class DogsVSCats():
IMG_SIZE = 50
CATS = "PetImages/Cat"
DOGS = "PetImages/Dog"
TESTING = "PetImages/Testing"
LABELS = {CATS: 0, DOGS: 1}
training_data = []
catcount = 0
dogcount = 0
def make_training_data(self):
for label in self.LABELS:
print(label)
for f in tqdm(os.listdir(label)):
if "jpg" in f:
try:
path = os.path.join(label, f)
img = cv2.imread(path, cv2.IMREAD_GRAYSCALE)
img = cv2.resize(img, (self.IMG_SIZE, self.IMG_SIZE))
self.training_data.append([np.array(img), np.eye(2)[self.LABELS[label]]]) # do something like print(np.eye(2)[1]), just makes one_hot
#print(np.eye(2)[self.LABELS[label]])
if label == self.CATS:
self.catcount += 1
elif label == self.DOGS:
self.dogcount += 1
except Exception as e:
pass
#print(label, f, str(e))
np.random.shuffle(self.training_data)
np.save("training_data.npy", self.training_data)
print('Cats:',dogsvcats.catcount)
print('Dogs:',dogsvcats.dogcount)
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 32, 5)
self.conv2 = nn.Conv2d(32, 64, 5)
self.conv3 = nn.Conv2d(64, 128, 5)
x = torch.randn(50,50).view(-1,1,50,50)
self._to_linear = None
self.convs(x)
self.fc1 = nn.Linear(self._to_linear, 512)
self.fc2 = nn.Linear(512, 2)
def convs(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2,2))
x = F.max_pool2d(F.relu(self.conv2(x)), (2,2))
x = F.max_pool2d(F.relu(self.conv3(x)), (2,2))
if self._to_linear is None:
self._to_linear = x[0].shape[0]*x[0].shape[1]*x[0].shape[2]
return x
def forward(self, x):
x = self.convs(x)
x = x.view(-1, self._to_linear)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return F.softmax(x, dim=1)
if torch.cuda.is_available():
device = torch.device("cuda:0") # you can continue going on here, like cuda:1 cuda:2....etc.
print("Running on the GPU")
else:
device = torch.device("cpu")
print("Running on the CPU")
net = Net().to(device)
if REBUILD_DATA:
dogsvcats = DogsVSCats()
dogsvcats.make_training_data()
training_data = np.load("training_data.npy", allow_pickle=True)
print(len(training_data))
optimizer = optim.Adam(net.parameters(), lr=0.001)
loss_function = nn.MSELoss()
X = torch.Tensor([i[0] for i in training_data]).view(-1, 50, 50)
X = X/255.0
y = torch.Tensor([i[1] for i in training_data])
VAL_PCT = 0.1
val_size = int(len(X)*VAL_PCT)
print(val_size)
train_X = X[:-val_size]
train_y = y[:-val_size]
test_X = X[-val_size:]
test_y = y[-val_size:]
print(len(train_X))
print(len(test_X))
def train(net):
BATCH_SIZE = 100
EPOCHS = 3
for epoch in range(EPOCHS):
for i in tqdm(range(0, len(train_X), BATCH_SIZE)):
batch_X = train_X[i:i+BATCH_SIZE].view(-1,1,50,50)
batch_y = train_y[i:i+BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
net.zero_grad()
outputs = net(batch_X)
loss = loss_function(outputs, batch_y)
loss.backward()
optimizer.step()
print(loss)
def test(net):
correct = 0
total = 0
with torch.no_grad():
for i in tqdm(range(len(test_X))):
real_class = torch.argmax(test_y[i]).to(device)
net_out = net(test_X[i].view(-1, 1, 50, 50).to(device))[0]
predicted_class = torch.argmax(net_out)
if predicted_class == real_class:
correct += 1
total += 1
print("Accuracy:", round(correct/total,3))
Результат:
Running on the GPU 24946 2494 22452 2494
С помощью приведенного выше кода мы можем обучить, а затем и протестировать нашу нейронную сеть, но не в той степени, в которой мы хотим. Начнем с изменения нашей функции train:
net = net.to(device)
def train(net):
BATCH_SIZE = 100
EPOCHS = 3
for epoch in range(EPOCHS):
for i in tqdm(range(0, len(train_X), BATCH_SIZE)):
batch_X = train_X[i:i+BATCH_SIZE].view(-1,1,50,50)
batch_y = train_y[i:i+BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
net.zero_grad()
outputs = net(batch_X)
matches = [torch.argmax(i)==torch.argmax(j) for i, j in zip(outputs, batch_y)]
in_sample_acc = matches.count(True)/len(matches)
loss = loss_function(outputs, batch_y)
loss.backward()
optimizer.step()
print(loss)
print("In-sample acc:",round(in_sample_acc, 2))
train(net)
Результат:
100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:15<00:00, 14.54it/s]
tensor(0.2380, device='cuda:0', grad_fn=<MseLossBackward>) In-sample acc: 0.58
100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:13<00:00, 16.40it/s]
tensor(0.2196, device='cuda:0', grad_fn=<MseLossBackward>) In-sample acc: 0.58
100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:13<00:00, 16.75it/s]
tensor(0.1804, device='cuda:0', grad_fn=<MseLossBackward>) In-sample acc: 0.71
Основное изменение состоит в следующем:
matches = [torch.argmax(i)==torch.argmax(j) for i, j in zip(outputs, batch_y)] in_sample_acc = matches.count(True)/len(matches)
Поскольку мы уже знаем целевые и фактические значения, всё, что нам нужно сделать, это сравнить их и вычислить некоторую процентную точность на выходе.
Это наша точность обучения. Здесь же мы также вычисляем и функцию потерь, которую тоже можем принять во внимание.
Помимо вычисления точности обучения за каждую эпоху, мы хотели бы видеть и данные тестирования за тот же период.
Некоторые наборы данных могут быть настолько большими, что мы хотели бы видеть результаты обучения на каждом шаге или хотя бы каждые 1000 шагов … и т. д. (бывает, что время прохождения одной эпохи может исчисляться днями или даже еще большими периодами времени).
Поскольку Pytorch дает нам довольно низкоуровневый доступ к настройкам нашего кода, все наши решения и ход работы полностью зависят от нас. Если вы хотите, чтобы ваши модели работали быстрее, вам следует выполнять проверочные тесты реже или с меньшими объемами данных. Например, наши тестовые данные содержат около 2500 примеров. Значит, нам нужно, чтобы наша модель делала 25 шагов при размере батча в 100.
Если бы мы делали это на каждом шаге, мы бы замедлили всю нашу нейронную сеть в 26 раз (делая 25 дополнительных шагов за 1 шаг обучения). Таким образом, если мы намерены проводить валидационное тестирование на каждом этапе, нам, вероятно, следует делать это с меньшими фрагментами наших тестовых данных.
Из-за этого у нас может возникнуть соблазн написать новую функцию следующего вида:
def batch_test(net):
BATCH_SIZE = 100
correct = 0
total = 0
with torch.no_grad():
#np.random.shuffle(test_X)
#np.random.shuffle(test_y)
batch_X = test_X[:BATCH_SIZE].view(-1,1,50,50)
batch_y = test_y[:BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
net.zero_grad()
outputs = net(batch_X)
matches = [torch.argmax(i)==torch.argmax(j) for i, j in zip(outputs, batch_y)]
acc = matches.count(True)/len(matches)
print("Test Accuracy:", round(acc, 3))
batch_test(net)
Результат:
Test Accuracy: 0.68
По крайней мере это то, что мы делали изначально, поэтому и делимся этим сейчас с вами.
Еще хотим поделиться одной ошибкой, которую мы совершили в начале написания данной функции (этот код в самом начале, сейчас закомментирован). Мы хотели перетасовать данные, чтобы вырезать случайный BATCH_SIZE из тестовых данных.
Мы сделали так и были крайне удивлены, что наша точность постоянно держалась в районе 50%. Только потом мы заметили, что перемешиваем данные по отдельности!
Правильным решением будет соединить данные при помощи функции zip, а затем уже перемешивать.
Размышляя подобным образом, мы задумались о повторениях. Обучение, тестирование, а теперь еще и пакетное тестирование использует весьма похожий код, и, черт побери, нам надо все это улучшить! А то наш код очень быстро раздувается.
Вот здесь Pytorch может стать проблемой для новичков (таких, как мы). Они начинают делать всевозможные глупые ошибки и забывают очевидные вещи, которые в общем-то знали. Как вариант — новички начинают привносить в свой код много сложных технических вещей.
Хорошо, давайте попробуем все это улучшить. Мы иногда склонны писать беспорядочный код, но, по крайней мере, всегда можем его исправить.
Есть соблазн назвать новую функцию fit, но она будет делать только прямой проход, следовательно, не всегда будет осуществлять обучение, при котором у нас меняются веса. Метод forward у нас уже есть, а конфликты нам не нужны. Ключевое слово pass мы также не можем использовать. Как же, черт возьми, нам ее назвать?
Назовем ее просто fwd_pass:
def fwd_pass(X, y, train=False):
if train:
net.zero_grad()
outputs = net(X)
matches = [torch.argmax(i)==torch.argmax(j) for i, j in zip(outputs, y)]
acc = matches.count(True)/len(matches)
loss = loss_function(outputs, y)
if train:
loss.backward()
optimizer.step()
return acc, loss
В любом случае, чтобы мы могли вычислить потери, нам нужно вычислять градиенты. Позже у нас может появиться функция, которая будет заниматься исключительно предсказаниями и делать это при помощи torch.no_grad. Единственное, что мы должны всегда проверять, это то, предназначены ли эти вычисления для обучения модели или нет. Потому что мы определенно не хотим изменять веса при обработке тестовой выборки. По этой причине мы будем по умолчанию использовать значение False. Если позволить нашим тестовым данным тайно обучать модель, потом это будет весьма сложно обнаружить.
Итак, давайте это проверим:
net = Net().to(device)
optimizer = optim.Adam(net.parameters(), lr=0.001)
loss_function = nn.MSELoss()
def train(net):
BATCH_SIZE = 100
EPOCHS = 3
for epoch in range(EPOCHS):
for i in tqdm(range(0, len(train_X), BATCH_SIZE)):
batch_X = train_X[i:i+BATCH_SIZE].view(-1,1,50,50)
batch_y = train_y[i:i+BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
acc, loss = fwd_pass(batch_X, batch_y, train=True)
print(f"Acc: {round(float(acc),2)} Loss: {round(float(loss),4)}")
# just to show the above working, and then get out:
if i == 5:
break
break
train(net)
Результат:
0%| | 0/225 [00:00<?, ?it/s]
Acc: 0.39 Loss: 0.2502
0%| | 0/225 [00:00<?, ?it/s]
Acc: 0.54 Loss: 0.2474
0%| | 0/225 [00:00<?, ?it/s]
Acc: 0.54 Loss: 0.2501
Пока все идет хорошо, но выводить это в консоль на каждом этапе немного глупо.
Вместо этого давайте просто будем логировать это в какой-нибудь файл. Так мы приблизимся к Tensorflow, которая использует для этого модуль Tensorboard, сохраняющий все статистику модели в отдельный файл.
С Pytorch вы также можете использовать что-то вроде tensorboardx, применяя таким образом Tensorboard к вашим моделям на Pytorch.
Мы долго думали над тем, зачем нам это все нужно.
Мы занимались глубоким обучением с Tensorflow примерно с того момента, когда он был впервые выпущен, и в 99% случаев отслеживали определенные скалярные величины при помощи Tensorboard.
Надо сказать, что хотя Tensorboard и весьма удобен, он зачастую отнимает много времени и ресурсов, чтобы показывать то, что вам нужно. Если он уже есть, то конечно грех им не воспользоваться, но специально встраивать его в Pytorch мы не будем. В действительности нам это не так уж и нужно. Вероятно, мы потратим больше времени на его настройку, чем на написание похожего кода.
Для начала мы просто воспользуемся Mathplotlib. Позже вы можете использовать для этих целей Dash или даже просто Pygal. Наконец, если хотите, попробуйте тот же tensorboardx! Это самое замечательное в Pytorch! Он полностью открыт и соответствует стилю Python. Вы можете делать все что хотите! Никто вас ни к чему не принуждает! Мы показываем вам лишь один из многих возможных вариантов.
Итак, теперь наша функция train примет следующий вид:
import time
MODEL_NAME = f"model-{int(time.time())}" # gives a dynamic model name, to just help with things getting messy over time.
net = Net().to(device)
optimizer = optim.Adam(net.parameters(), lr=0.001)
loss_function = nn.MSELoss()
def train(net):
BATCH_SIZE = 100
EPOCHS = 3
with open("model.log", "a") as f:
for epoch in range(EPOCHS):
for i in tqdm(range(0, len(train_X), BATCH_SIZE)):
batch_X = train_X[i:i+BATCH_SIZE].view(-1,1,50,50)
batch_y = train_y[i:i+BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
acc, loss = fwd_pass(batch_X, batch_y, train=True)
#print(f"Acc: {round(float(acc),2)} Loss: {round(float(loss),4)}")
f.write(f"{MODEL_NAME},{int(time.time())},in_sample,{round(float(acc),2)},{round(float(loss),4)}\n")
# just to show the above working, and then get out:
if i == 5:
break
break
train(net)
Результат:
0%| | 0/225 [00:00<?, ?it/s] 0%| | 0/225 [00:00<?, ?it/s] 0%| | 0/225 [00:00<?, ?it/s]
Открыв файл model.log, мы увидим:
model-1570487772,1570487772,in_sample,0.61,0.2497 model-1570487772,1570487773,in_sample,0.54,0.2508 model-1570487772,1570487773,in_sample,0.46,0.25
Кажется, работает. Со временем мы могли бы сделать эти журналы более нарядными, а позже, возможно, использовать что-то вроде sqlite для сохранения различных моделей и тому подобного. Но на данный момент того, что есть, более чем достаточно.
import time
MODEL_NAME = f"model-{int(time.time())}" # gives a dynamic model name, to just help with things getting messy over time.
net = Net().to(device)
optimizer = optim.Adam(net.parameters(), lr=0.001)
loss_function = nn.MSELoss()
def train(net):
BATCH_SIZE = 100
EPOCHS = 3
with open("model.log", "a") as f:
for epoch in range(EPOCHS):
for i in tqdm(range(0, len(train_X), BATCH_SIZE)):
batch_X = train_X[i:i+BATCH_SIZE].view(-1,1,50,50)
batch_y = train_y[i:i+BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
acc, loss = fwd_pass(batch_X, batch_y, train=True)
#print(f"Acc: {round(float(acc),2)} Loss: {round(float(loss),4)}")
f.write(f"{MODEL_NAME},{round(time.time(),3)},in_sample,{round(float(acc),2)},{round(float(loss),4)}\n")
# just to show the above working, and then get out:
if i == 5:
break
break
train(net)
Результат:
0%| | 0/225 [00:00<?, ?it/s] 0%| | 0/225 [00:00<?, ?it/s] 0%| | 0/225 [00:00<?, ?it/s]
Единственное изменение здесь — f.write (f "{MODEL_NAME}, {round (time.time (), 3)}, in_sample, {round (float (acc), 2)}, {round (float (loss), 4)} \ n "), где мы просто получаем десятичные дроби из time.time (). Теперь мы можем построить график:
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
model_name = "model-1570490221" # grab whichever model name you want here. We could also just reference the MODEL_NAME if you're in a notebook still.
def create_acc_loss_graph(model_name):
contents = open("model.log", "r").read().split("\n")
times = []
accuracies = []
losses = []
for c in contents:
if model_name in c:
name, timestamp, sample_type, acc, loss = c.split(",")
times.append(timestamp)
accuracies.append(acc)
losses.append(loss)
fig = plt.figure()
ax1 = plt.subplot2grid((2,1), (0,0))
ax2 = plt.subplot2grid((2,1), (1,0), sharex=ax1)
ax1.plot(times, accuracies, label="in_samp_acc")
ax1.legend(loc=2)
ax2.plot(times,losses, label="in_samp_loss")
ax2.legend(loc=2)
plt.show()
create_acc_loss_graph(model_name)
Ок, неплохо. Здесь можно было бы многое улучшить, но пока для нас просто важно видеть, что у нас все под контролем и мы может отслеживать то, что хотим.
Далее, мы хотим отслеживать точность и функцию потерь. Опять же, мы можем отследить это на основе выборочной информации любое количество раз и разными способами. Как часто мы хотим это рассчитывать? На каком количестве данных? Все зависит от нас (вас!).
На 225 шагах мы могли бы проверять каждый шаг, но это значительно увеличило бы время обучения. Мы не реализуем алгоритм обратного распространения ошибки, но все же вычисляем потери и тому подобное. Насколько данные будут детализированы, зависит, опять же, от вас. Мы сейчас собираемся использовать случайный BATCH_SIZE при валидации данных модели каждые 10 шагов, а затем еще произвести тестирование модели в самом конце. Таким образом, мы можем написать следующую функцию тестирования:
def test(size=32):
X, y = test_X[:size], test_y[:size]
val_acc, val_loss = fwd_pass(X.view(-1, 1, 50, 50).to(device), y.to(device))
return val_acc, val_loss
val_acc, val_loss = test(size=100)
print(val_acc, val_loss)
Результат:
0.49 tensor(0.2522, device='cuda:0', grad_fn=<MseLossBackward>)
Отлично, теперь давайте будем запускать эту функцию каждые 10 шагов:
import time
MODEL_NAME = f"model-{int(time.time())}" # gives a dynamic model name, to just help with things getting messy over time.
net = Net().to(device)
optimizer = optim.Adam(net.parameters(), lr=0.001)
loss_function = nn.MSELoss()
def train(net):
BATCH_SIZE = 100
EPOCHS = 3
with open("model.log", "a") as f:
for epoch in range(EPOCHS):
for i in tqdm(range(0, len(train_X), BATCH_SIZE)):
batch_X = train_X[i:i+BATCH_SIZE].view(-1,1,50,50)
batch_y = train_y[i:i+BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
acc, loss = fwd_pass(batch_X, batch_y, train=True)
#print(f"Acc: {round(float(acc),2)} Loss: {round(float(loss),4)}")
#f.write(f"{MODEL_NAME},{round(time.time(),3)},train,{round(float(acc),2)},{round(float(loss),4)}\n")
# just to show the above working, and then get out:
if i % 10 == 0:
val_acc, val_loss = test(size=100)
f.write(f"{MODEL_NAME},{round(time.time(),3)},{round(float(acc),2)},{round(float(loss), 4)},{round(float(val_acc),2)},{round(float(val_loss),4)}\n")
train(net)
Результат:
100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 9.40it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.03it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.99it/s]
Как видите, время обучения одной эпохи увеличилось с ~14 секунд до 25 секунд. У нас, вероятно, есть немало вещей, которые мы могли бы оптимизировать. Полный контроль над подобными вещами — это и подарок, и проклятие. У вас есть возможность делать все именно так, как вы хотите, и, возможно, быстрее. …но вы также можете сильно замедлиться, если не будете осторожны. Мы можем поговорить об оптимизации нашего журнала позже. А пока давайте посмотрим, что у нас есть. Название нашей последней модели было model-1570499409.
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
model_name = MODEL_NAME #"model-1570499409" # grab whichever model name you want here. We could also just reference the MODEL_NAME if you're in a notebook still.
def create_acc_loss_graph(model_name):
contents = open("model.log", "r").read().split("\n")
times = []
accuracies = []
losses = []
val_accs = []
val_losses = []
for c in contents:
if model_name in c:
name, timestamp, acc, loss, val_acc, val_loss = c.split(",")
times.append(float(timestamp))
accuracies.append(float(acc))
losses.append(float(loss))
val_accs.append(float(val_acc))
val_losses.append(float(val_loss))
fig = plt.figure()
ax1 = plt.subplot2grid((2,1), (0,0))
ax2 = plt.subplot2grid((2,1), (1,0), sharex=ax1)
ax1.plot(times, accuracies, label="acc")
ax1.plot(times, val_accs, label="val_acc")
ax1.legend(loc=2)
ax2.plot(times,losses, label="loss")
ax2.plot(times,val_losses, label="val_loss")
ax2.legend(loc=2)
plt.show()
create_acc_loss_graph(model_name)
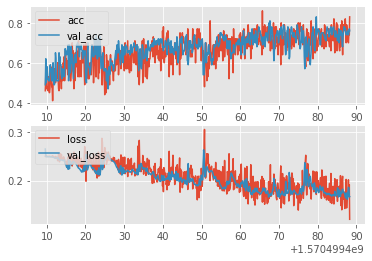
import time
MODEL_NAME = f"model-{int(time.time())}" # gives a dynamic model name, to just help with things getting messy over time.
net = Net().to(device)
optimizer = optim.Adam(net.parameters(), lr=0.001)
loss_function = nn.MSELoss()
print(MODEL_NAME)
def train(net):
BATCH_SIZE = 100
EPOCHS = 30
with open("model.log", "a") as f:
for epoch in range(EPOCHS):
for i in tqdm(range(0, len(train_X), BATCH_SIZE)):
batch_X = train_X[i:i+BATCH_SIZE].view(-1,1,50,50)
batch_y = train_y[i:i+BATCH_SIZE]
batch_X, batch_y = batch_X.to(device), batch_y.to(device)
acc, loss = fwd_pass(batch_X, batch_y, train=True)
#print(f"Acc: {round(float(acc),2)} Loss: {round(float(loss),4)}")
#f.write(f"{MODEL_NAME},{round(time.time(),3)},train,{round(float(acc),2)},{round(float(loss),4)}\n")
# just to show the above working, and then get out:
if i % 50 == 0:
val_acc, val_loss = test(size=100)
f.write(f"{MODEL_NAME},{round(time.time(),3)},{round(float(acc),2)},{round(float(loss), 4)},{round(float(val_acc),2)},{round(float(val_loss),4)},{epoch}\n")
train(net)
Результат:
model-1570499915
100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.79it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.92it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.78it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.07it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.96it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.04it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.98it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.02it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.02it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.92it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.02it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.95it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.04it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.88it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.83it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.93it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.83it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.03it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.92it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.00it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.02it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.94it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.76it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.71it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.85it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.99it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:24<00:00, 9.05it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.96it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.71it/s] 100%|a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^a-^| 225/225 [00:25<00:00, 8.79it/s]
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
model_name = "model-1570499915" # grab whichever model name you want here. We could also just reference the MODEL_NAME if you're in a notebook still.
def create_acc_loss_graph(model_name):
contents = open("model.log", "r").read().split("\n")
times = []
accuracies = []
losses = []
val_accs = []
val_losses = []
for c in contents:
if model_name in c:
name, timestamp, acc, loss, val_acc, val_loss, epoch = c.split(",")
times.append(float(timestamp))
accuracies.append(float(acc))
losses.append(float(loss))
val_accs.append(float(val_acc))
val_losses.append(float(val_loss))
fig = plt.figure()
ax1 = plt.subplot2grid((2,1), (0,0))
ax2 = plt.subplot2grid((2,1), (1,0), sharex=ax1)
ax1.plot(times, accuracies, label="acc")
ax1.plot(times, val_accs, label="val_acc")
ax1.legend(loc=2)
ax2.plot(times,losses, label="loss")
ax2.plot(times,val_losses, label="val_loss")
ax2.legend(loc=2)
plt.show()
create_acc_loss_graph(model_name)
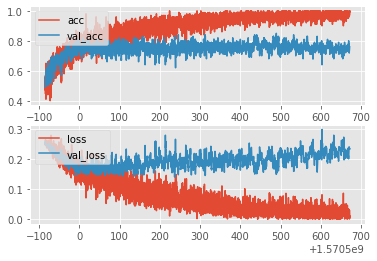
Отлично, теперь мы ясно видим, что после 4-5 эпох все начинает ухудшаться (каждая эпоха это примерно 25 секунд, время у нас отложено по оси Х) . Значит, сейчас мы хорошо понимаем, что обучать нашу модель надо не более 5 эпох. Также хорошо видно, что после 8 эпохи все становиться совсем плохо.
Надеюсь, этот пример помог вам визуализировать процесс обучения нейронных сетей и основную статистику, которую нужно отслеживать. Кроме того, вы могли заметить, насколько хорошо нейронные сети могут сначала обобщать информацию, но позже переобучаться и просто ее запоминать.
На этом у нас пока все. Благодаря примеру в нашей статье вы можете рисовать все, что захотите, продолжая использовать Matplotlib (который имеет большое количество причудливых функций, таких как ось multi-y, и множество других настроек), или использовать другие модули для построения графиков. Или применить tensorboardx.
Далее мы собираемся рассмотреть еще некоторые интересные вопросы, а именно рекуррентные нейронные сети. Они могут быть полезны для некоторых задач, которые сверточные сети еще не умеют решать, например для задач машинного перевода.

