Сегодня мы поговорим про то, как построить математический график при помощи языка Python за 10 минут. Мы рассмотрим построение параметрических кривых в трехмерном и двумерном пространстве с использованием различных примеров.
У многих из нас со школьной скамьи остались не самые приятные воспоминания о математике. Кто-то воспринимал её как необходимое зло: сложное и скучное, но обязательное. Кто-то же отказывался понимать математику от слова совсем.
Так или иначе, но наше школьное образование было ориентировано скорее на запоминание и заучивание, а не на размышления. По большому счету не было никакой мотивации разбираться в основах математики или в том, как она на самом деле работает. Идея заключалась в том, чтобы просто узнать, какие задачи решает определенная формула, запомнить правильный набор шагов и воспроизвести все это на экзамене.
Однако математика намного обширнее и интереснее того, что мы учили в школе. Если взять, например, кинематику, можно увидеть настоящую магию математики. Кинематика известна как «геометрия движения» – это изучение взаимодействия между движущимися телами во времени. Хотя бы раз увидите такое визуальное представление математических функций — и они оживут для вас. Возможно, в тот момент вы почувствуете, что впервые понимаете их правильно.
Итак, давайте научимся самостоятельно моделировать данные и начнем писать собственные скрипты. Сегодня мы поговорим о параметрических кривых и как их строить, используя Python и такие библиотеки, как NumPy, SymPy и Matplotlib.
Построение параметрических кривых
Параметрические кривые поистине завораживают! Если говорить простым языком, параметрическую кривую можно понимать как след, оставляемый движением частицы в пространстве. Говоря более формально, этот след моделируется функцией, определяемой от интервала I до различных точек в пространстве E.
Для трехмерного случая, если x, y и z заданы как функции переменной t в I (это параметр), мы получаем уравнения x = f(t), y = g(t) и z = h(t). Оценивая каждое значение параметра t в каждом из этих уравнений, мы получаем точку p(t) = (x(t),y(t),z(t)) в пространстве. Проделав эту процедуру для значений t, меняющихся в интервале I, мы получим параметрическую кривую.
Проведя небольшое исследование, попробовав несколько моделей вручную и потратив много часов на работу над сценарием, мы нашли решение. Оно выглядит следующим образом:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
t = sp.Symbol('t')
function_x = sp.sympify('sin(t)')
function_y = sp.sympify('cos(t)')
function_z = sp.sympify('t**2')
interval = np.arange(0, 100, 0.1)
x_values = [function_x.subs(t, value) for value in interval]
y_values = [function_y.subs(t, value) for value in interval]
z_values = [function_z.subs(t, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show()
Приведенный выше скрипт позволяет нам генерировать графики для параметрических кривых. К примеру, вот так выглядит график параметрической спирали p(t) = (sin(t),cos(t),sqrt(t3)), для интервала от 0 до 100.
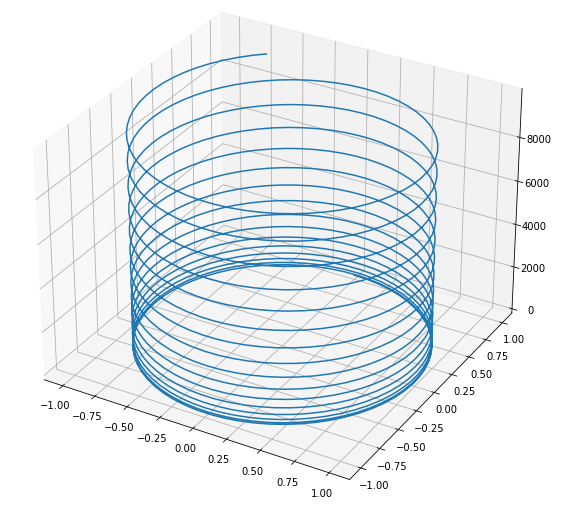
Как работает скрипт
Скрипт, который мы привели выше, использует такие библиотеки, как SymPy, NumPy и Matplotlib. Давайте разберемся со всем по порядку.
SymPy — это библиотека Python для символьной математики. Она стремится стать полнофункциональной системой компьютерной алгебры (CAS). При этом сохраняется максимально простой код (а значит, понятный и масштабируемый). Библиотека SymPy, кстати, полностью написана на Python.
NumPy — это основной пакет для научных вычислений в Python. Эта библиотека предоставляет:
- объекты многомерного массива,
- различные производные объекты (такие как маскированные массивы и матрицы)
- набор подпрограмм для быстрых операций с массивами, включая математические и логические, манипуляции с фигурами, сортировку, выборку, ввод-вывод, дискретные преобразования Фурье, основные операции линейной алгебры, основные статистические операции и случайное моделирование.
И последняя библиотека из нашего списка — Matplotlib. Это обширная библиотека для создания статических, анимированных и интерактивных визуализаций на Python.
Подготовка
Чтобы использовать перечисленные выше библиотеки в нашем скрипте, мы должны сначала установить их на свой компьютер, выполнив следующую инструкцию в терминале:
pip install numpy sympy matplotlib
Теперь, когда библиотеки установлены, мы можем импортировать их в нашу программу:
import sympy as sp import numpy as np import matplotlib.pyplot as plt
Построение графика трехмерной параметрической кривой
Символьные вычисления в SymPy выполняются с помощью символов. Переменные SymPy являются объектами класса Symbols. Выражение t = sp.Symbol('t') присваивает символ t переменной t, с которой мы теперь можем работать как с математической переменной.
Выглядит это следующим образом:
t = sp.Symbol('t')
print(t ** 2)
>>> t ^ 2
В рамках этой задачи нам нужно работать с составными выражениями, хранящимися в строке. Поэтому нам нужно сделать преобразование строки в математическое выражение понятным для SymPy. Для этого мы используем функцию sympify.sp.sympify(expression), которая преобразует параметрическое выражение в общее математическое выражение.
К примеру, наш код будет выглядеть так:
function_z = sp.sympify('t^2')
print(function_z + 2)
>>> t ^ 2 + 2
Теперь переменная function_z содержит математическое выражение t2+2.
Следующим шагом является возможность оценить параметр t внутри математического выражения. Функция subs() в SymPy позволит нам оценить выражение с заданным значением. Мы можем использовать его следующим образом: expression.subs(t, value).
Наш код будет выглядеть следующим образом:
value = function_z.subs(t, 5) print(value) >>> 5 ^ 2 = 25
Поскольку мы говорим о параметрических функциях, нас интересует оценка функции на последовательности вещественных значений в пределах интервала. Для этого мы используем функцию arange() в NumPy.
Функция np.arange(start, stop, step) создает массив NumPy со значениями в интервале (start,stop) с приращением шага, то есть мы идем от start до stop-1 с определенным шагом step.
Наш код будет выглядеть так:
interval = np.arange(0, 10, 1) print(interval) >>> array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
После создания массива интервалов нам нужно перебрать значения t и оценить каждое значение внутри функции. Для этого мы будем использовать генератор списков в Python и функцию subs() библиотеки SimPy.
О генераторах списков можно почитать в статье «Генераторы списков в Python для начинающих».
Функция subs() получает символ t (который мы сохранили в переменной t) и значение каждого из элемента в качестве параметров.
Выглядит это примерно следующим образом:
z_values = [function_z.subs(t, value) for value in interval] print(z_values) >>> [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
Мы повторяем эту процедуру для значений x_values и y_values и таким образом получаем массивы со значениями для построения.
Наконец, с помощью библиотеки Matplotlib мы создаем график, соответствующий нашей параметрической кривой. В трехмерном случае, чтобы указать Matplotlib, что мы хотим сделать трехмерный график, мы используем следующий оператор:
ax = plt.axes(projection='3d')
Кроме того, мы можем заменить функции и интервал на новые и получить самые разные кривые. Давайте попробуем еще раз, но с другими значениями.
Например, напишем следующий код:
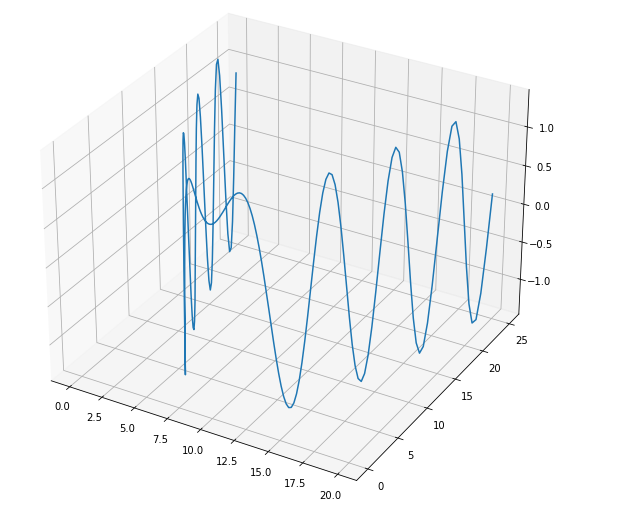
function_x = sp.sympify('2*t + 10')
function_y = sp.sympify('t**2')
function_z = sp.sympify('sin(t**2) + cos(t**2)')
interval = np.arange(-5, 5, 0.05)
Запустим наш код и получим такой график:
Немного поэкспериментируем
Давайте немного поэкспериментируем с нашим кодом: попробуем различные значения и посмотрим, что получится. С помощью параметрических кривых можно создать множество фигур. Некоторые комбинации могут генерировать кривые с уникальной симметрией и красотой.
Если вы хотите поиграть со скриптом самостоятельно, можете открыть эту ссылку и заменить значения для function_x, function_y, function_z и interval.
К примеру, можно взять следующий код:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('t')
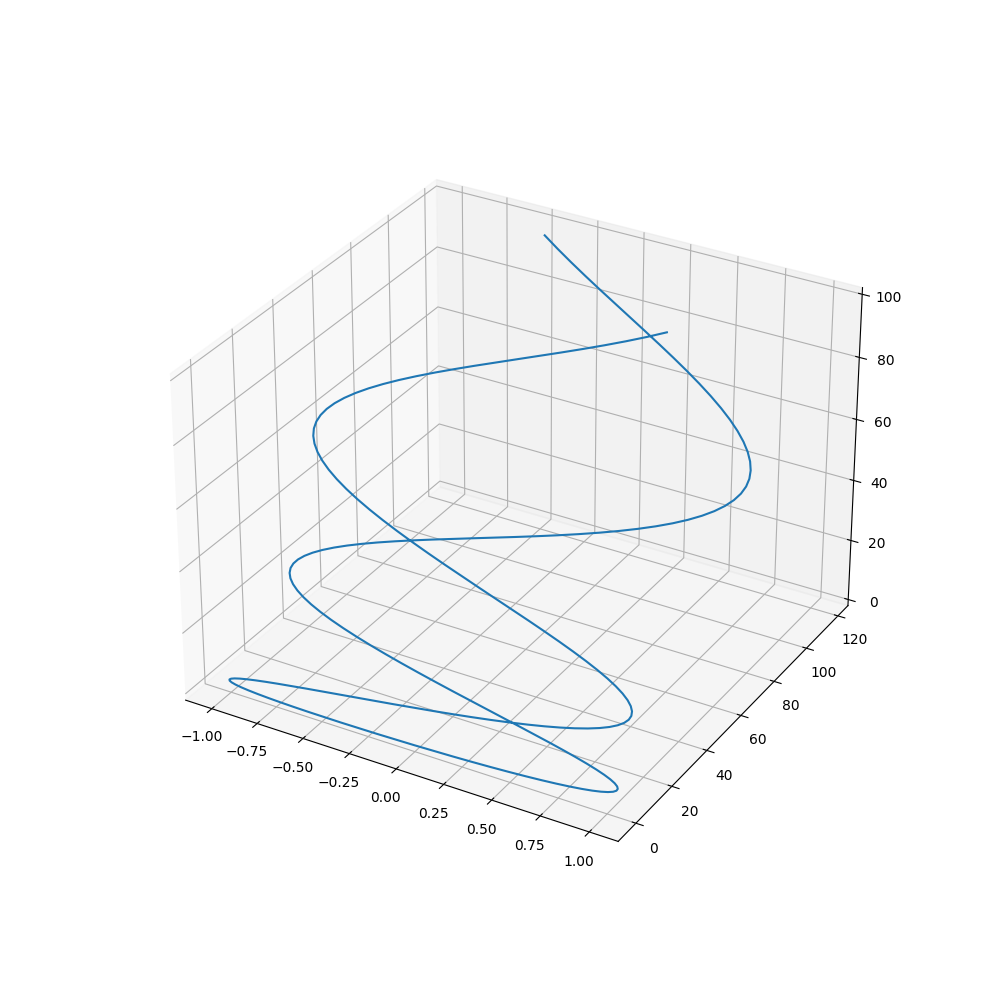
function_x = sp.sympify('sin(t)')
function_y = sp.sympify('t^2+2*t')
function_z = sp.sympify('t^2')
interval = np.arange(-10, 10, 0.1)
x_values = [function_x.subs(symbol_x, value) for value in interval]
y_values = [function_y.subs(symbol_x, value) for value in interval]
z_values = [function_z.subs(symbol_x, value) for value in interval]
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot(x_values, y_values, z_values)
plt.show()
Запустив его, мы получим такой результат:
Поиграйтесь сами и посмотрите, какие удивительные параметрические кривые можно создать!
Построение 2D параметрических кривых
С некоторыми модификациями данный скрипт также можно использовать и для построения двумерных параметрических кривых.
Например, давайте построим двумерный график, полученный путем оценки выражения x = t − 1,6 ∗ cos(24 ∗ t) и y = t − 1,6 ∗ sin(25 ∗ t) на интервале I=[1.5,20.5].
Выглядеть это будет примерно следующим образом:
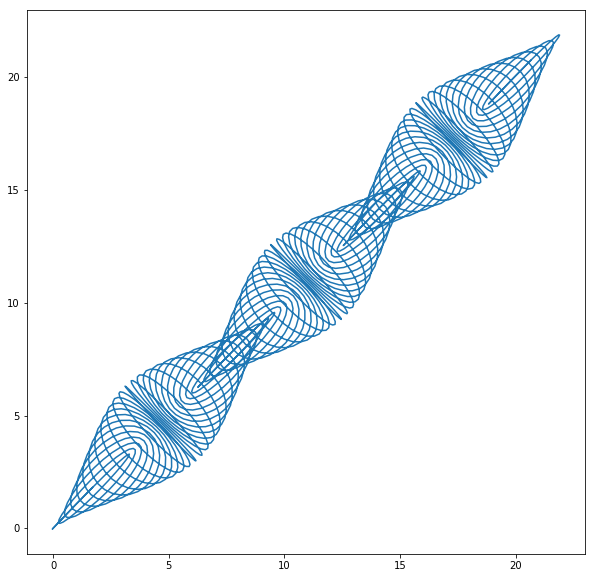
Для того, чтобы смоделировать параметрическую кривую, показанную выше, можно воспользоваться следующим скриптом:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
t = sp.Symbol('t')
function_x = sp.sympify('t - 1.6*cos(24*t)')
function_y = sp.sympify('t - 1.6*sin(25*t)')
interval = np.arange(1.5, 20.5, 0.01)
x_values = [function_x.subs(t, value) for value in interval]
y_values = [function_y.subs(t, value) for value in interval]
plt.figure(figsize=(10, 10))
plt.plot(x_values, y_values)
plt.show()
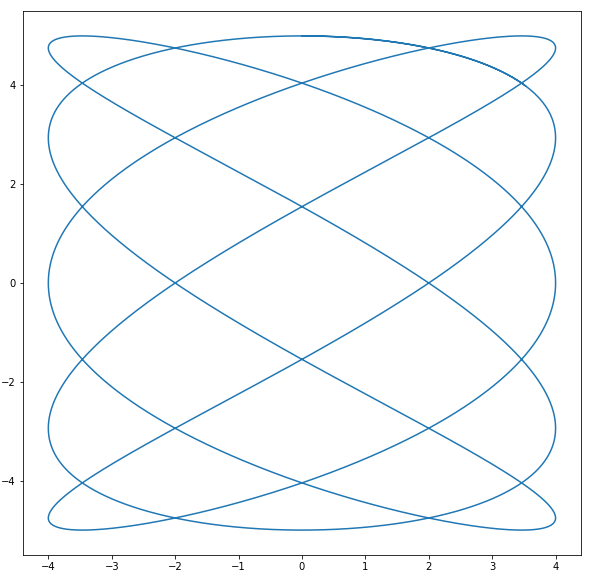
Давайте проверим наш код с другими функциями и новым интервалом. К примеру, возьмем следующие значения:
function_x = sp.sympify('4*sin(5*t)')
function_y = sp.sympify('5*cos(3*t)')
interval = np.arange(0, 6.5, 0.001)
Запустим наш скрипт и получим следующий график:
Теперь давайте проделаем это ещё раз, но уже с новыми значениями:
function_x = sp.sympify('cos(16*t) + (cos(6*t) / 2) + (sin(10*t) / 3)')
function_y = sp.sympify('sin(16*t) + (sin(6*t) / 2) + (cos(10*t) / 3)')
interval = np.arange(0, 3.16, 0.01)
Тогда результат будет таким:
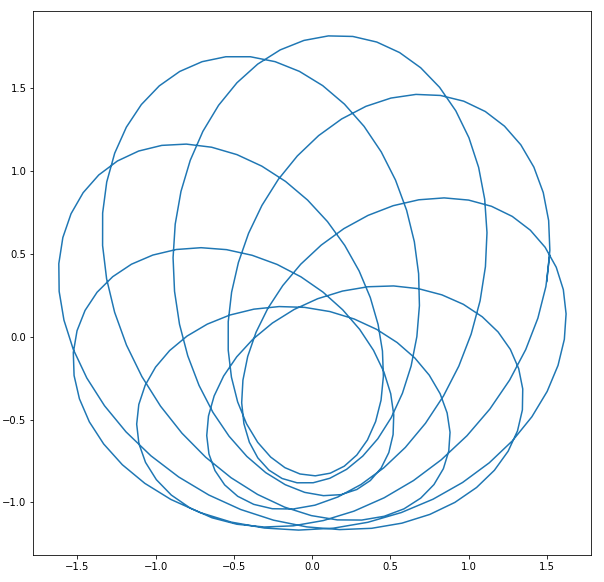
Удивительно! Не правда ли?
Построение математических функций
Как только мы закончили написание скрипта для моделирования параметрических кривых, приходит осознание, что с помощью всего нескольких строк кода мы можем создать плоттер для математических функций как в двух, так и в трех измерениях! Невероятно! Это же так удобно!
К примеру, давайте рассмотрим скрипт для построения графиков математических функций в двух и трех измерениях в интервале от a до b. То есть, консоль запросит у пользователя как функцию, так и значения a и b для интервала. Вот такой код у нас получится:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp.sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image,
rstride=1, cstride=1, cmap='viridis')
plt.show()
function = input('>> Enter the function: ')
a_value = float(input('>> Enter the [a, ] value: '))
b_value = float(input('>> Enter the [, b] value: '))
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
Вы можете протестировать приведенный выше скрипт здесь. Запустите скрипт и введите свою конфигурацию функции и интервала.
Например, возьмем следующий код:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp.sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.show()
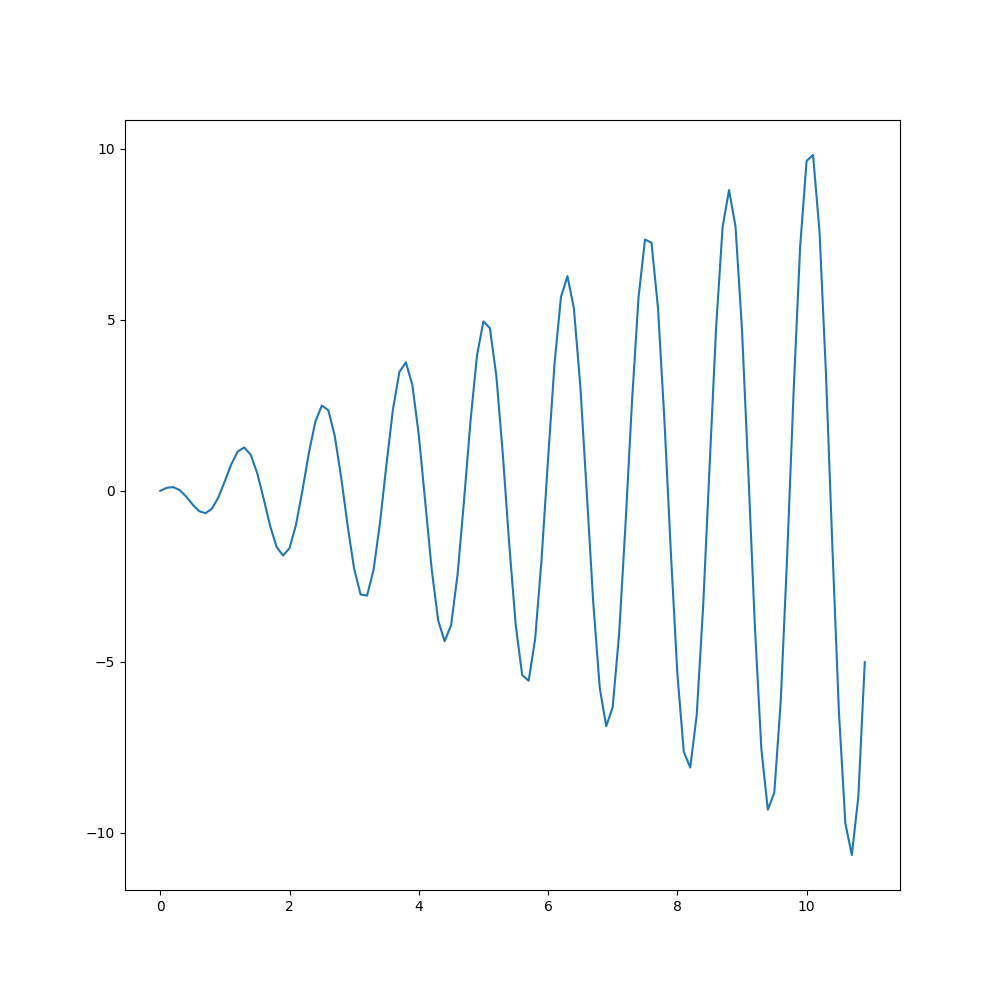
function = "x*cos(5*x)"
a_value = 0
b_value = 10
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
Запустим его и получим следующий результат:
А теперь давайте поменяем значения на следующие:
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
symbol_x = sp.Symbol('x')
symbol_y = sp.Symbol('y')
def get_vector(a, b):
return np.arange(a, b + 1, 0.1)
def plot_2d_function(function, a, b):
# Create the sympy function f(x)
f_x = sp.sympify(function)
# Create domain and image
domain_x = get_vector(a, b)
image = [f_x.subs(symbol_x, value) for value in domain_x]
# Plot the 2D function graph
fig = plt.figure(figsize=(10, 10))
plt.plot(domain_x, image)
plt.show()
def plot_3d_function(function, a, b):
# Create sympy function f(x, y)
f_xy = sp.lambdify((symbol_x, symbol_y), sp.sympify(function))
# Create domains and image
domain_x = get_vector(a, b)
domain_y = get_vector(a, b)
domain_x, domain_y = np.meshgrid(domain_x, domain_y)
image = f_xy(domain_x, domain_y)
# Plot the 3D function graph
fig = plt.figure(figsize=(10, 10))
ax = plt.axes(projection='3d')
ax.plot_surface(domain_x, domain_y, image, rstride=1, cstride=1, cmap='viridis')
plt.show()
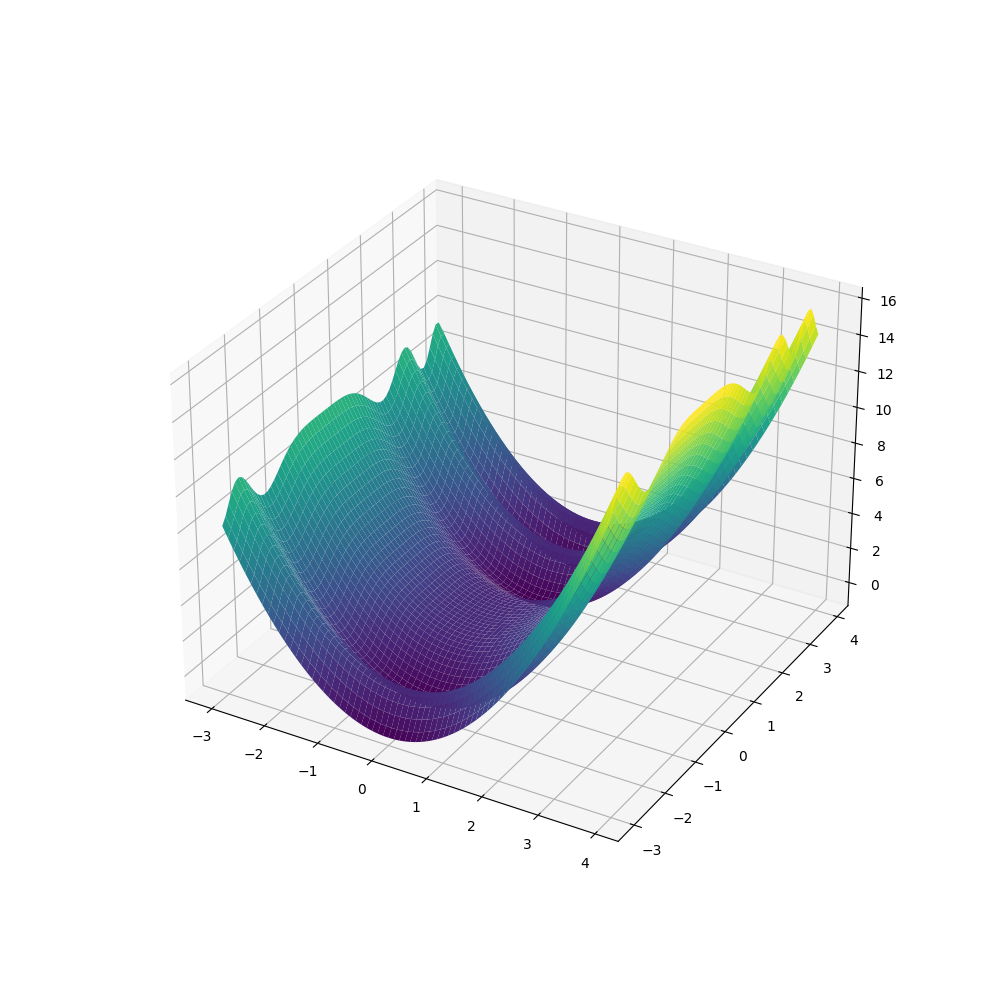
function = "x**2 + cos(y**2)"
a_value = -3
b_value = 3
if "x" and not "y" in function:
plot_2d_function(function, a_value, b_value)
elif "x" and "y" in function:
plot_3d_function(function, a_value, b_value)
else:
print("You must enter a function in terms of x and/or y")
Если мы это запустим, то получим такой график:
Заключение
Что ж, вот вы и дошли до конца этой статьи, поздравляем! Сегодня мы обсудили, как построить математический график на Python всего за 10 минут. Мы поговорили про построение различных параметрических кривых в двумерном и трёхмерном пространстве и разобрали процесс построения на примерах. Теперь вы видите, какой завораживающей на самом деле может быть математика! Кроме того, построение параметрических кривых, как вы понимаете, не такой уж и сложный процесс.
Надеемся, данная статья была вам полезна! Успехов в написании кода!
Перевод статьи «How to Plot Mathematical Functions in 10 Lines of Python».

