Сортировка слиянием на Python

Программа будет сортировать список методом слияния (Merge Sort).

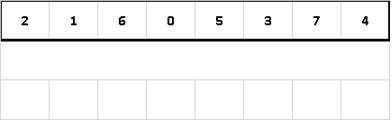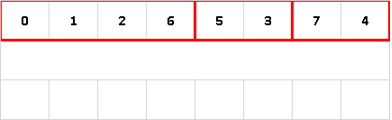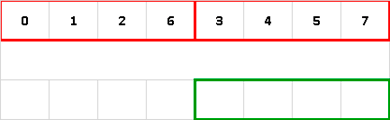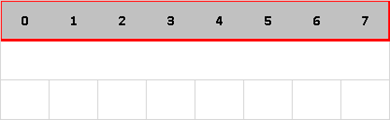
Суть сортировки

1. Сортируемый массив разбивается на две части примерно одинакового размера.
2. Каждая из получившихся частей сортируется отдельно, например, тем же самым алгоритмом.
3. Два упорядоченных массива половинного размера соединяются в один.

Сложность сортировки по времени

1. Худшая O(n log n)
2. Средняя O(n log n)
3. Лучшая O(n log n)

Шаги к правильному решению

1. Создадим функцию merge_sort, которая принимает на вход список и 2 переменные: start и end.
2. Функция merge_sort будет сортировать список от start до end-1 индексов.
3. Если end-start не больше 1, выходим.
4. Иначе, устанавливаем mid = (start+end)//2 (округляет до меньшего 15//2=7)
5. Вызываем merge_sort(alist, start, mid).
6. Вызываем merge_sort(alist, mid, end).
7. Вызываем merge_list(alist, start, mid, end).
8. Функция принимает список и 3 параметра, полагает, что список отсортирован от start до mid-1 и от mid до end-1, смерживает их и образует новый сортированный список от start до end-1.

def merge_sort(alist, start, end):
    '''Sorts the list from indexes start to end - 1 inclusive.'''
    if end - start > 1:
        mid = (start + end)//2
        merge_sort(alist, start, mid)
        merge_sort(alist, mid, end)
        merge_list(alist, start, mid, end)
 
def merge_list(alist, start, mid, end):
    left = alist[start:mid]
    right = alist[mid:end]
    k = start
    i = 0
    j = 0
    while (start + i < mid and mid + j < end):
        if (left[i] <= right[j]):
            alist[k] = left[i]
            i = i + 1
        else:
            alist[k] = right[j]
            j = j + 1
        k = k + 1
    if start + i < mid:
        while k < end:
            alist[k] = left[i]
            i = i + 1
            k = k + 1
    else:
        while k < end:
            alist[k] = right[j]
            j = j + 1
            k = k + 1
 
 
alist = input('Enter the list of numbers: ').split()
alist = [int(x) for x in alist]
merge_sort(alist, 0, len(alist))
print('Sorted list: ', end='')
print(alist)